题目内容
3. 如图,在四边形ABCD中,∠DAB=$\frac{π}{3}$,AD:AB=2:3,BD=$\sqrt{7}$,AB⊥BC.
如图,在四边形ABCD中,∠DAB=$\frac{π}{3}$,AD:AB=2:3,BD=$\sqrt{7}$,AB⊥BC.(1)求sin∠ABD的值;
(2)若∠BCD=$\frac{2π}{3}$,求CD的长.
分析 (1)设AD=2x,AB=3x,由余弦定理求出AD=2,AB=3,再由正弦定理能求出sin∠ABD.
(2)由sin(∠ABD+∠CBD)=sin$\frac{π}{2}$,得sin∠CBD=cos∠ABD,求出sin$∠CBD=\frac{2\sqrt{7}}{7}$,由此利用正弦定理能求出CD.
解答 解:(1)设AD=2x,AB=3x,
由余弦定理得:cos$\frac{π}{3}$=$\frac{4{x}^{2}+9{x}^{2}-7}{2×2x×3x}$=$\frac{1}{2}$,
解得x=1,∴AD=2,AB=3,
∴由正弦定理得:$\frac{sin∠ABD}{2}=\frac{sin\frac{π}{3}}{\sqrt{7}}$,
解得sin∠ABD=$\frac{\sqrt{21}}{7}$.
(2)sin(∠ABD+∠CBD)=sin$\frac{π}{2}$,∴sin∠CBD=cos∠ABD,
cos$∠ABD=\sqrt{1-\frac{21}{49}}$=$\frac{2\sqrt{7}}{7}$,∴sin$∠CBD=\frac{2\sqrt{7}}{7}$,
由正弦定理得$\frac{CD}{sin∠CBD}=\frac{BD}{sin\frac{2π}{3}}$,解得CD=$\frac{4\sqrt{3}}{3}$.
点评 本题考角的正弦值的求法,考查三角形边长的求法,考查正弦定理、余弦定理、诱导公式、同角三角函数关系式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 .
. 的值;
的值; 的面积为
的面积为 ,
, .
. ,
, ,则
,则 ( )
( ) B.
B.
 D.
D.
 的底面
的底面 是矩形,平面
是矩形,平面 平面
平面 ,
,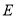 是
是 的中点,且
的中点,且 ,
, .
.
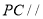 平面
平面 ;
; 的体积.
的体积.