题目内容
设双曲线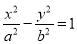 (
(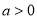 ,
,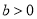 )的虚轴长为
)的虚轴长为 ,焦距为
,焦距为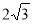 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.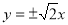 B.
B.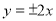 C.
C.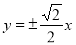 D.
D.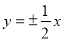
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
题目内容
设双曲线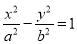 (
(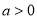 ,
,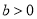 )的虚轴长为
)的虚轴长为 ,焦距为
,焦距为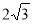 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.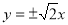 B.
B.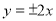 C.
C.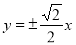 D.
D.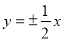
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案