题目内容
若
(3x2+kx)dx=2,则k= .
| ∫ | 1 0 |
考点:定积分
专题:导数的概念及应用
分析:根据微积分基本定理解得即可.
解答:
解:
(3x2+kx)dx=(x3+
kx2)|
=1+
k=2,
解得k=2,
故答案为:2
| ∫ | 1 0 |
| 1 |
| 2 |
1 0 |
| 1 |
| 2 |
解得k=2,
故答案为:2
点评:本题主要考查了定积分的计算,属于基础题.

练习册系列答案
相关题目
执行如图所示的程序框图,如果输入的x,y,N的值分别为1,2,3,则输出的S=( )
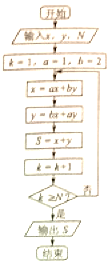

| A、27 | B、81 | C、99 | D、577 |
若a=0.53,b=30.5,c=log30.5,则a,b,c,的大小关系是( )
| A、b>a>c |
| B、b>c>a |
| C、a>b>c |
| D、c>b>a |
已知数列{an}的前n项和Sn=n2-6n,数列{|an|}的前n项和Tn,则
的最小值是( )
| Tn |
| n |
A、6
| ||
B、
| ||
C、
| ||
| D、3 |
若函数f(x)=lg(x2+ax-a-1)在区间[2,+∞)上单调递增,则实数a的取值范围是( )
| A、(-3,+∞) |
| B、[-3,+∞) |
| C、(-4,+∞) |
| D、[-4,+∞) |
已知函数y=f(x)的定义域为[2,4],则函数y=f(2x)定义域为( )
| A、[0,1] |
| B、[1,2] |
| C、[4,16] |
| D、[2,4] |