题目内容
6．已知长方体ABCD-A1B1C1D1，点E、F分别是上底面A1B1C1D1和面CC1D1D的中心，求其中x，y，z的值．（1）$\overrightarrow{A{C}_{1}}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$+z$\overrightarrow{C{C}_{1}}$；
（2）$\overrightarrow{AE}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$+z$\overrightarrow{C{C}_{1}}$；
（3）$\overrightarrow{AF}$=x$\overrightarrow{BA}$+y$\overrightarrow{BC}$+z$\overrightarrow{{C}_{1}C}$．
分析 利用空间向量三角形法则结构长方体结构特征求解．
解答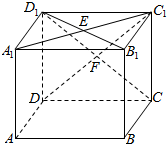 
解：（1）∵长方体ABCD-A1B1C1D1，点E、F分别是上底面A1B1C1D1和面CC1D1D的中心，
$\overrightarrow{A{C}_{1}}$=$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{C{C}_{1}}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$+z$\overrightarrow{C{C}_{1}}$，
∴x=1，y=1，z=1．
（2）$\overrightarrow{AE}$=$\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}E}$=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}$+$\overrightarrow{C{C}_{1}}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$+z$\overrightarrow{C{C}_{1}}$，
∴x=$\frac{1}{2}$，y=$\frac{1}{2}$，z=1．
（3）$\overrightarrow{AF}$=$\overrightarrow{AD}+\overrightarrow{DF}$=$\frac{1}{2}\overrightarrow{AB}$+$\overrightarrow{BC}$+$\frac{1}{2}\overrightarrow{C{C}_{1}}$=-$\frac{1}{2}\overrightarrow{BA}$+$\overrightarrow{BC}$+$\frac{1}{2}\overrightarrow{C{C}_{1}}$=x$\overrightarrow{BA}$+y$\overrightarrow{BC}$+z$\overrightarrow{{C}_{1}C}$，
∴x=-$\frac{1}{2}$，y=1，z=$\frac{1}{2}$．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意空间向量三角形法则的灵活运用．
口算小状元口算速算天天练系列答案| A． | $\frac{3}{2}$ | B． | 2 | C． | $\frac{{3\sqrt{2}}}{2}$ | D． | $2\sqrt{2}$ |