题目内容
已知x>0,y>0,x+y=1,则
+
的最小值是 .
| 1 |
| x+1 |
| 1 |
| y+1 |
考点:基本不等式
专题:不等式
分析:利用基本不等式求出x+y=1时,xy≤
;再求
+
的最小值.
| 1 |
| 4 |
| 1 |
| x+1 |
| 1 |
| y+1 |
解答:
解:∵x>0,y>0,x+y=1,
∴xy≤(
)2=
,当且仅当x=y=
时,“=”成立;
∴
+
≥2
=2
=2
≥2
=2×
=
,当且仅当x=y=
时“=”成立.
故答案为:
.
∴xy≤(
| x+y |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
∴
| 1 |
| x+1 |
| 1 |
| y+1 |
|
=2
|
=2
|
|
=2×
| 2 |
| 3 |
=
| 4 |
| 3 |
| 1 |
| 2 |
故答案为:
| 4 |
| 3 |
点评:本题考查了基本不等式的灵活应用问题,解题时应注意不等式等号成立的条件是什么,是基础题目.

练习册系列答案
相关题目
直线m⊥平面α,垂足是O,正四面体ABCD的棱长为4,点C在平面α上运动,点B在直线m上运动,则点O到直线AD的距离的取值范围是( )
A、[
| ||||||||
B、[2
| ||||||||
C、[
| ||||||||
D、[3
|
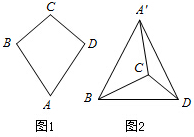 如图1,已知四边形ABCD的对角线AC与BD互相垂直,∠A=60°,∠C=90°,CD=CB=2,将△ABD沿BD折起,得到三棱锥A′-BCD,如图2.
如图1,已知四边形ABCD的对角线AC与BD互相垂直,∠A=60°,∠C=90°,CD=CB=2,将△ABD沿BD折起,得到三棱锥A′-BCD,如图2.