题目内容
若
=2，则2sinθcosθ=（ ）
| sinθ+cosθ |
| sinθ-cosθ |
A、-
| ||
B、
| ||
C、±
| ||
D、
|
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：已知等式左边分子分母除以cosθ，利用同角三角函数间的基本关系化简求出tanθ的值，原式利用二倍角的正弦函数公式化简，再利用万能公式变形，把tanθ的值代入计算即可求出值．
解答：
解：已知等式变形得：
=2，即tanθ=3，
则原式=sin2θ=
=
=
，
故选：B．
| tanθ+1 |
| tanθ-1 |
则原式=sin2θ=
| 2tanθ |
| 1+tan2θ |
| 6 |
| 10 |
| 3 |
| 5 |
故选：B．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
如图，节日花坛中有5个区域，要把4种不同颜色的花分别种植到这5个区域中，要求相同颜色的花不能相邻栽种，一共有多少种种植方案？已知O为△ABC的外心，|
|=16，|
|=10
，若
=x
+y
，且32x+25y=25，则|
|=（ ）
| AB |
| AC |
| 2 |
| AO |
| AB |
| AC |
| OA |
| A、8 | B、10 | C、12 | D、14 |
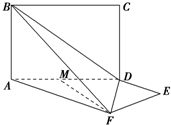如图，平面ABCD⊥平面ADEF，其中ABCD为矩形，ADEF为梯形，AF∥DE，AF⊥FE，AF=AD=2DE=2，M为线段AD的中点．