题目内容
不等式logax≥(x-1)2恰有2个整数解,则a的取值范围是 .
考点:指、对数不等式的解法
专题:函数的性质及应用
分析:作出函数y=(x-1)2的图象,若不等式logax≥(x-1)2恰有2个整数解,则确定点A在对数图象的下方,而B在图象的上方即可.
解答:
 解:作出函数y=(x-1)2的图象,
解:作出函数y=(x-1)2的图象,
若0<a<1,由图象知,不满足条件.
若a>1,则(1,0)是函数logax和y=(x-1)2的一个公共点,
若不等式logax≥(x-1)2恰有2个整数解,
则A(2,1)是不等式的一个解,而B(3,4)不是不等式的解,
则满足
,
即
,
解得
<a≤2,
故答案为:(
,2]
 解:作出函数y=(x-1)2的图象,
解:作出函数y=(x-1)2的图象,若0<a<1,由图象知,不满足条件.
若a>1,则(1,0)是函数logax和y=(x-1)2的一个公共点,
若不等式logax≥(x-1)2恰有2个整数解,
则A(2,1)是不等式的一个解,而B(3,4)不是不等式的解,
则满足
|
即
|
解得
| 4 | 3 |
故答案为:(
| 4 | 3 |
点评:本题主要考查方程根的个数的应用,利用数形结合以及对数函数和二次函数的图象和性质是解决本题的关键.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
若
=2,则2sinθcosθ=( )
| sinθ+cosθ |
| sinθ-cosθ |
A、-
| ||
B、
| ||
C、±
| ||
D、
|
若a,b,c>0且a(a+b+c)+bc=4-2
,则2a+b+c的最小值为( )
| 3 |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
已知m、n是三次函数f(x)=
x3+
ax2+2bx(a、b∈R)的两个极值点,且m∈(0,1),n∈(1,2),则
的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| b+3 |
| a+2 |
A、(-∞,
| ||
B、(
| ||
| C、(-4,3) | ||
| D、(-∞,-4)∪(3,+∞) |
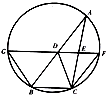 如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明:
如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明: 如图,在直角梯形ABCD中,AD∥BC,BC⊥CD=4,已知AD=5,BC=4,CD=
如图,在直角梯形ABCD中,AD∥BC,BC⊥CD=4,已知AD=5,BC=4,CD=