题目内容
在平面直角坐标系中,二元方程f(x,y)=0的曲线为C,若存在一个定点A和一个定角θ(θ∈(0,2π)),使得曲线C上的任意一点以A为中心顺时针(或逆时针)旋转角θ,所得到的图形与原曲线重合,则称曲线C为旋转对称曲线,给出以下方程及其对应的曲线,其中是旋转对称曲线的是 (填上你认为正确的曲线).
C1:
+y2=1; C2:
•
=0;
C3:x2-y=0(x∈[-2,2]); C4:y-cosx=0(x∈[0,π])
C1:
| x2 |
| 4 |
| 1-|x| |
| 1-|y| |
C3:x2-y=0(x∈[-2,2]); C4:y-cosx=0(x∈[0,π])
考点:曲线与方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:利用旋转对称曲线的定义,确定一个定点A和一个定角θ(θ∈(0,2π)),即可得出结论.
解答:
解:由题意,C1:
+y2=1,存在一个定点A(0,0)和一个定角θ=π;
C2:
•
=0,存在一个定点A(0,0)和一个定角θ=
;
C3:x2-y=0(x∈[-2,2])是轴对称图形,不是中心对称图形;
C4:y-cosx=0(x∈[0,π]),存在一个定点A(
,0)和一个定角θ=π,
故答案为:C1,C2,C4.
| x2 |
| 4 |
C2:
| 1-|x| |
| 1-|y| |
| π |
| 2 |
C3:x2-y=0(x∈[-2,2])是轴对称图形,不是中心对称图形;
C4:y-cosx=0(x∈[0,π]),存在一个定点A(
| π |
| 2 |
故答案为:C1,C2,C4.
点评:本题考查曲线与方程,考查旋转对称曲线的定义,正确理解旋转对称曲线的定义是关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
若
=2,则2sinθcosθ=( )
| sinθ+cosθ |
| sinθ-cosθ |
A、-
| ||
B、
| ||
C、±
| ||
D、
|
若a,b,c>0且a(a+b+c)+bc=4-2
,则2a+b+c的最小值为( )
| 3 |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
 如图,在直角梯形ABCD中,AD∥BC,BC⊥CD=4,已知AD=5,BC=4,CD=
如图,在直角梯形ABCD中,AD∥BC,BC⊥CD=4,已知AD=5,BC=4,CD=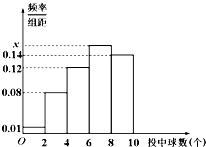 为鼓励中青年教师参加篮球运动,校工会组织了100名中青年教师进行投篮活动,每人投10次,投中情况绘成频率分布直方图(如图),则这100 名教师投中6至8个球的人数为
为鼓励中青年教师参加篮球运动,校工会组织了100名中青年教师进行投篮活动,每人投10次,投中情况绘成频率分布直方图(如图),则这100 名教师投中6至8个球的人数为