题目内容
设x，y想，满足约束条件
，若目标函数z=ax+by（a＞0，b＞0）的最大值为12，则
+
的最小值为（ ）
|
| 3 |
| a |
| 2 |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、4 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式对应的平面区域，利用线性规划的知识先求出a，b的关系，然后利用基本不等式求
+
的最小值．
| 3 |
| a |
| 2 |
| b |
解答：
解：由z=ax+by（a＞0，b＞0）得y=-
x+
，
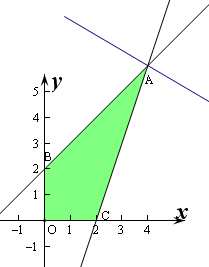
作出可行域如图：
∵a＞0，b＞0，
∴直线y=-
x+
的斜率为负，且截距最大时，z也最大．
平移直线y=-
x+
，由图象可知当y=-
x+
经过点A时，
直线的截距最大，此时z也最大．
由
，解得
，即A（4，6）．
此时z=4a+6b=12，
即
+
=1，
则
+
=（
+
）（
+
）=1+1+
+
≥2+2
=4，
当且仅当
=
时取=号，
故选：D
解：由z=ax+by（a＞0，b＞0）得y=-| a |
| b |
| z |
| b |
作出可行域如图：
∵a＞0，b＞0，
∴直线y=-
| a |
| b |
| z |
| b |
平移直线y=-
| a |
| b |
| z |
| b |
| a |
| b |
| z |
| b |
直线的截距最大，此时z也最大．
由
|
|
此时z=4a+6b=12，
即
| a |
| 3 |
| b |
| 2 |
则
| 3 |
| a |
| 2 |
| b |
| 3 |
| a |
| 2 |
| b |
| a |
| 3 |
| b |
| 2 |
| 3b |
| 2a |
| 2a |
| 3b |
|
当且仅当
| 3b |
| 2a |
| 2a |
| 3b |
故选：D
点评：本题主要考查线性规划的应用以及基本不等式的应用，利用数形结合是解决线性规划题目的常用方法．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
在平面直角坐标系xOy中，如果菱形OABC的边长为2，点A在x轴上，则菱形内（不含边界）整点（横纵坐标都是整数的点）个数的取值集合是（ ）
| A、{1，2} |
| B、{1，2，3} |
| C、{0，1，2} |
| D、{0，1，2，3} |
某堆雪在融化过程中，其体积V（单位：m3）与融化时间t（单位：h）近似满足函数关系：
已知函数y=logb（x-a）（b＞0且b≠1）的图象如图所示，那么函数y=a+sinbx的图象可能是（ ）
