Question

20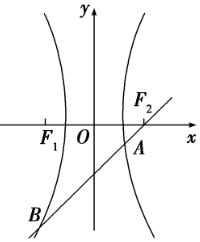．过双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的右焦点作倾斜角为45°的弦AB．求：
（1）弦AB的中点C到右焦点F₂的距离；
（2）弦AB的长．

Answer 1

分析 （1）求出直线AB的方程，代入双曲线方程，求出C的坐标，即可求弦AB的中点C到右焦点F₂的距离；
（2）利用弦长公式求弦AB的长．

解答 解：（1）由已知，AB的方程为y=x-5，
将其代入$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1，得7x²+90x-369=0．设A（x₁，y₁），B（x₂，y₂），
则x₁+x₂=-$\frac{90}{7}$，∴$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{45}{7}$，解得$\frac{{y}_{1}+{y}_{2}}{2}$=-$\frac{80}{7}$
AB的中点C的坐标为（-$\frac{45}{7}$，-$\frac{80}{7}$）．
于是|CF|=$\sqrt{（-\frac{45}{7}-5）^{2}+（-\frac{80}{7}-0）^{2}}$=$\frac{80\sqrt{2}}{7}$；
（2）弦AB的长=$\sqrt{1+1}•\sqrt{（-\frac{90}{7}）^{2}+4×\frac{369}{7}}$=$\frac{224}{7}$．

点评 本题考查双曲线的方程与性质，考查直线与双曲线的位置关系，考查学生的计算能力，属于中档题．