题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{x+2(x≤-1)}\\{{x}^{2}(-1<x<2)}\\{2x(x≥2)}\end{array}\right.$(1)求f(2),f($\frac{1}{2}$),f[f(-1)];
(2)若f(a)=3,求a的值.
分析 (1)由函数性质能求出f(2),f($\frac{1}{2}$),f[f(-1)];
(2)当a≤1时,f(a)=a+2=3;当-1<a<2时,f(a)=a2=3;当a≥2时,f(a)=2a=3.由此能求出a的值.
解答 解:(1)∵函数f(x)=$\left\{\begin{array}{l}{x+2(x≤-1)}\\{{x}^{2}(-1<x<2)}\\{2x(x≥2)}\end{array}\right.$
∴f(2)=2×2=4,
f($\frac{1}{2}$)=($\frac{1}{2}$)2=$\frac{1}{4}$,
f(-1)=-1+2=1,
f[f(-1)]=f(1)=12=1.
(2)当a≤1时,f(a)=a+2=3,解得a=1,成立;
当-1<a<2时,f(a)=a2=3,解得a=$\sqrt{3}$或a=-$\sqrt{3}$(舍);
当a≥2时,f(a)=2a=3,解得a=$\frac{3}{2}$,不成立.
∴a的值为1或$\sqrt{3}$.
点评 本题考查函数值的求法,考查实数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
15.若复数z满足$\frac{{{{(1-i)}^2}}}{z}$=1+i(i为虚数单位),则复数z位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知圆的方程为x2+y2=1,则点P(3,2)( )
| A. | 是圆心 | B. | 在圆上 | C. | 在圆内 | D. | 在圆外 |
10.设α,β,γ为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题,其中真命题有( )
①若m?α,n?β,α⊥β,则m⊥n;
②若m⊥α,n∥β且α∥β,则m⊥n;
③若α∥β,l?α,则l∥β;
④若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.
①若m?α,n?β,α⊥β,则m⊥n;
②若m⊥α,n∥β且α∥β,则m⊥n;
③若α∥β,l?α,则l∥β;
④若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
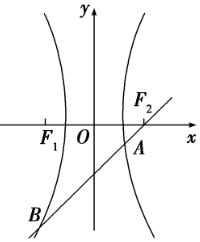 过双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的右焦点作倾斜角为45°的弦AB.求:
过双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的右焦点作倾斜角为45°的弦AB.求: 如图,在正四棱锥P-AMDE,底面AMDE的边长为2,侧棱PA=$\sqrt{5}$,B,C分别
如图,在正四棱锥P-AMDE,底面AMDE的边长为2,侧棱PA=$\sqrt{5}$,B,C分别