题目内容
2. 棱长为1的正方形ABCD-A1B1C1D1中,给出以下结论:
棱长为1的正方形ABCD-A1B1C1D1中,给出以下结论:①AB1⊥CD1;
②四面体B1D1CA的体积为$\frac{1}{3}$;
③(S${\;}_{△AD{D_1}}}}$)2+(S${\;}_{△CD{D_1}}}}$)2+(S△ADC)2=(S${\;}_{△AC{D_1}}}}$)2.
其中结论正确的为①②③.(写出所有正确的结论的序号).
分析 由题意画出图形,利用异面直线所成角的概念判断①;求出四面体B1D1CA的体积判断②;通过计算说明③正确.
解答 解:如图,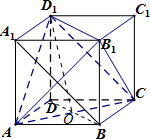
连接A1B,∵ABCD-A1B1C1D1是正方体,
∴A1B∥CD1,且A1B⊥AB1,
则AB1⊥CD1,故①正确;
${V}_{{B}_{1}{D}_{1}CA}={V}_{ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1}}-4{V}_{{B}_{1}-ABC}$=$1-4×\frac{1}{3}×\frac{1}{2}×1×1=\frac{1}{3}$,故②正确;
连接BD交AC于O,连接D1O,则D1O⊥AC,则$O{D}_{1}=\sqrt{{1}^{2}+(\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{6}}{2}$,
∵(S${\;}_{△AD{D_1}}}}$)2+(S${\;}_{△CD{D_1}}}}$)2+(S△ADC)2=$3×(\frac{1}{2}×1×1)^{2}=\frac{3}{4}$,
(S${\;}_{△AC{D_1}}}}$)2=$(\frac{1}{2}×\sqrt{2}×\frac{\sqrt{6}}{2})^{2}=\frac{3}{4}$,
∴(S${\;}_{△AD{D_1}}}}$)2+(S${\;}_{△CD{D_1}}}}$)2+(S△ADC)2=(S${\;}_{△AC{D_1}}}}$)2,故③正确.
故答案为:①②③.
点评 本题考查棱柱的结构特征,考查空间想象能力和思维能力,考查了计算能力,是中档题.

练习册系列答案
相关题目
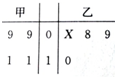 从巍山县庙街镇一所小学的甲、乙两个班级分别随机抽取4名学生的年龄制作出如右所示茎叶图,乙纪录中有一个数据模糊,无法确认,以X表示.
从巍山县庙街镇一所小学的甲、乙两个班级分别随机抽取4名学生的年龄制作出如右所示茎叶图,乙纪录中有一个数据模糊,无法确认,以X表示.