题目内容
11.化简:$\begin{array}{l}\frac{{sin(2π-α)cos(π+α)cos(\frac{π}{2}+α)cos(\frac{11}{2}π-α)}}{{cos(π-α)sin(3π-α)sin(-π-α)sin(\frac{9}{2}π+α)}}$-$\frac{sin(-α)}{cos(-α)}\end{array}$.分析 利用诱导公式直接化简求解即可.
解答 解:原式=$\begin{array}{l}\frac{{-sin(α)({-cosα})({-sinα})({-sinα})}}{-cosαsinαsinαcosα}-\frac{-sinα}{cosα}\end{array}$
=$-\frac{sin(α)}{cosα}-\frac{-sinα}{cosα}=0$.
点评 本题考查诱导公式的应用,三角函数化简求值,考查计算能力.

练习册系列答案
相关题目
1.已知抛物线y=ax2+bx+c通过点P(1,1),且在点Q(2,-1)处的切线平行于直线y=x-3,则抛物线方程为( )
| A. | y=3x2-11x+9 | B. | y=3x2+11x+9 | C. | y=3x2-11x-9 | D. | y=-3x2-11x+9 |
6.如图,ABCD-A1B1C1D1为正方体,则下列结论错误的是( )
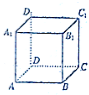

| A. | A1C⊥B1D1 | B. | B1D1∥平面BDC1 | ||
| C. | A1C⊥平面BDC1 | D. | 异面直线AD与BC1所成的角为30° |
3.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x-1),则x<0时,f(x)的解析式为( )
| A. | f(x)=x(x+1) | B. | f(x)=-x(x+1) | C. | f(x)=x(1-x) | D. | f(x)=x2-1 |
 棱长为1的正方形ABCD-A1B1C1D1中,给出以下结论:
棱长为1的正方形ABCD-A1B1C1D1中,给出以下结论: