题目内容
13.设正项等比数列{an}的前n项和为Sn,记bn=$\frac{{{a}_{n+1}}^{2}}{{a}_{n}}$.且数列{bn}的前n项和为Tn(1)求证:{bn}是等比数列;
(2)若Sn<Tn恒成立,求等比数列{an}公比q的取值范围.
分析 (1)由题意可设数列{an}首项a1>0,公比q>0,求出bn,由等比数列的定义证明{bn}是等比数列;
(2)分析q=1时与已知矛盾;当q≠1时,由Sn<Tn即可求得等比数列{an}公比q的取值范围.
解答 证明:(1)∵数列{an}是正项等比数列,则首项a1>0,公比q>0,
${b}_{n}=\frac{{{a}_{n+1}}^{2}}{{a}_{n}}=\frac{({a}_{1}{q}^{n})^{2}}{{a}_{1}{q}^{n-1}}={a}_{1}{q}^{n+1}$,
$\frac{{b}_{n+1}}{{b}_{n}}=\frac{{a}_{1}{q}^{n+2}}{{a}_{1}{q}^{n+1}}=q$,为定值,
∴{bn}是等比数列;
解:(2)若q=1,则an=a1,bn=a1,Sn=Tn,与已知矛盾,∴q≠1;
由Sn<Tn,得$\frac{{S}_{n}}{{T}_{n}}<1$,
即$\frac{\frac{{a}_{1}(1-{q}^{n})}{1-q}}{\frac{{a}_{1}{q}^{2}(1-{q}^{n})}{1-q}}<1$,得q2>1,
即q<-1(舍)或q>1.
点评 本题考查数列递推式,考查了等比关系的确定,训练了不等式的解法,是中档题.

练习册系列答案
相关题目
3.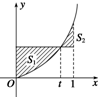 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )
 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )| A. | ($\frac{1}{2}$,1) | B. | ($\frac{1}{2}$,2] | C. | [0,1] | D. | (1,2] |
4.已知集合A={x|x2-4=0},B={1,2},则A∩B=( )
| A. | 2 | B. | {-2,2} | C. | {2} | D. | ∅ |
1.已知抛物线y=ax2+bx+c通过点P(1,1),且在点Q(2,-1)处的切线平行于直线y=x-3,则抛物线方程为( )
| A. | y=3x2-11x+9 | B. | y=3x2+11x+9 | C. | y=3x2-11x-9 | D. | y=-3x2-11x+9 |
8.若直线(1+a)x+y+1=0与圆(x-1)2+y2=1相切,则a的值为( )
| A. | 1,-1 | B. | 2,-2 | C. | 1 | D. | -1 |
18.已知x≥0,y≥0,x2+y2=4,μ=x•y-4(x+y)+10,μ的最值情况是( )
| A. | 有最大值2,最小值2(2-$\sqrt{2}$)2 | B. | 有最大值2,最小值0 | ||
| C. | 有最大值10,最小值2(2-$\sqrt{2}$)2 | D. | 最值不存在 |
6.如图,ABCD-A1B1C1D1为正方体,则下列结论错误的是( )
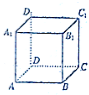

| A. | A1C⊥B1D1 | B. | B1D1∥平面BDC1 | ||
| C. | A1C⊥平面BDC1 | D. | 异面直线AD与BC1所成的角为30° |
 棱长为1的正方形ABCD-A1B1C1D1中,给出以下结论:
棱长为1的正方形ABCD-A1B1C1D1中,给出以下结论: