题目内容
在平面直角坐标系xOy中,已知
=(-1,t),
=(2,2),若∠ABO=90°,则t=( )
| OA |
| OB |
| A、2 | B、4 | C、5 | D、8 |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:由向量的运算可得
的坐标,由∠ABO=90°可得
•
=0,可得t的方程,解方程可得.
| AB |
| AB |
| OB |
解答:
解:∵
=(-1,t),
=(2,2),
∴
=
-
=(3,2-t)
又∵∠ABO=90°,
∴
⊥
,
∴
•
=3×2+2×(2-t)=0
解得t=5
故选:C.
| OA |
| OB |
∴
| AB |
| OB |
| OA |
又∵∠ABO=90°,
∴
| AB |
| OB |
∴
| AB |
| OB |
解得t=5
故选:C.
点评:本题考查平面向量的数量积与垂直的关系,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某中学进行模拟考试有80个考室,每个考室30个考生,每个考试座位号按1~30号随机抽取试卷进行评分标准,每个考场抽取座位号为15号考生试卷质检,这种抽样方法是( )
| A、简单随机抽样 | B、系统抽样 |
| C、分层抽样 | D、分组抽样 |
有下列命题:
①两组对应边相等的三角形是全等三角形;
②“若xy=0,则|x|+|y|=0”的逆命题;
③“若a>b,则2x•a>2x•b”的否命题;
④“矩形的对角线互相垂直”的逆否命题.
其中真命题共有( )
①两组对应边相等的三角形是全等三角形;
②“若xy=0,则|x|+|y|=0”的逆命题;
③“若a>b,则2x•a>2x•b”的否命题;
④“矩形的对角线互相垂直”的逆否命题.
其中真命题共有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列命题中,真命题是( )
| A、?x0∈R,ex0≤0 | ||||
| B、?x∈R,2x>x2 | ||||
C、双曲线x2-y2=1的离心率为
| ||||
D、双曲线x2-
|
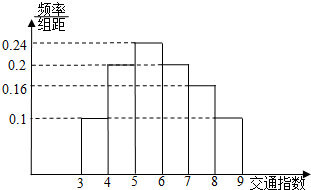
 下列是容量为100的样本的频率分布直方图,则样本数据落在范围〔6,10〕内的频数值为
下列是容量为100的样本的频率分布直方图,则样本数据落在范围〔6,10〕内的频数值为