题目内容
若不等式组
(其中a>0)表示的平面区域的面积是9.
(1)求a的值
(2)求
的最小值,及此时x与y的值.
|
(1)求a的值
(2)求
| y |
| x-3 |
考点:简单线性规划
专题:不等式的解法及应用
分析:(1)作出不等式组对应的平面区域,利用平面区域的面积建立条件关系即可求出a的值.
(2)利用
的几何意义,即可利用数形结合即可得到结论.
(2)利用
| y |
| x-3 |
解答:
解:(1)作出不等式组对应的平面区域如图:(阴影部分).
三个交点为C(-1,0)、B(a,a+1)、A(a,-a-1),
因为a>0,面积S=为
•(a+1)(2a+2)=9,
所以a=2.
(2)
为点(x,y)与(3,0)两点间的斜率,
由图象知(x,y)落在B(2,3)时,最小-3,
此时x=2,y=3.

三个交点为C(-1,0)、B(a,a+1)、A(a,-a-1),
因为a>0,面积S=为
| 1 |
| 2 |
所以a=2.
(2)
| y-0 |
| x-3 |
由图象知(x,y)落在B(2,3)时,最小-3,
此时x=2,y=3.
点评:本题主要考查线性规划以及直线斜率的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
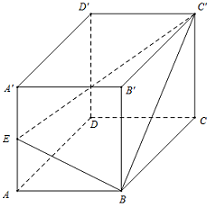 已知正方体ABCD-A′B′C′D′中,E是AA′棱的中点.求平面BEC′与平面ABCD所成的角的余弦值.
已知正方体ABCD-A′B′C′D′中,E是AA′棱的中点.求平面BEC′与平面ABCD所成的角的余弦值. 如图所示,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,求DF•DB的值.
如图所示,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,求DF•DB的值.