题目内容
5.经过点(2,0)且与曲线$y=\frac{1}{x}$相切的直线方程为( )| A. | x+4y+2=0 | B. | x+4y-2=0 | C. | x+y+2=0 | D. | x+y-2=0 |
分析 设切点为(x0,y0),则y0=$\frac{1}{{x}_{0}}$,由于直线l经过(2,0),推出切线的斜率,再根据导数的几何意义求出曲线在点x0处的切线斜率,便可建立关于x0的方程.求出x0,然后求解切线方程.
解答 解:设直线l:y=k(x-1).∵曲线$y=\frac{1}{x}$,∴y′=-$\frac{1}{{x}^{2}}$,∴$y′{|}_{x={x}_{0}}$=-$\frac{1}{{{x}_{0}}^{2}}$
设曲线的切点(x0,y0)(x0≠0),则k=$\frac{{y}_{0}-0}{{x}_{0}-2}$,
∴-$\frac{1}{{{x}_{0}}^{2}}$=$\frac{1}{{{x}_{0}}^{2}-2{x}_{0}}$,∵x0≠0,∴x0=1,∴k=-1,
故直线l的方程为:x+y-2=0.
故选:D.
点评 此题考查学生会利用导数求曲线上过某点切线方程的斜率,会根据一点坐标和斜率写出直线的方程,是一道综合题.

练习册系列答案
相关题目
19.若数列{an}为等差数列,Sn为其前n项和,且a2=3a4-6,则S9等于( )
| A. | 54 | B. | 50 | C. | 27 | D. | 25 |
20.若集合A={x|x>0},B={x|y=ln(x-1)},则A∩B等于( )
| A. | (1,+∞) | B. | (0,1) | C. | [1,+∞) | D. | (-∞,1) |
17.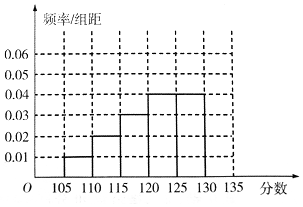 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
(Ⅰ)补全所给的频率分布直方图,并求n,x,y的值;
(Ⅱ)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取9份进行展出,并从9份试卷中选出两份作为优秀试卷,优秀试卷在[115,120)中的分数记为ξ,求随机变量ξ的分布列及期望.
 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:| 组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
| 第一组 | [105,110] | 15 | 0.3 |
| 第二组 | [110,115) | 30 | 0.3 |
| 第三组 | [115,120) | x | 0.4 |
| 第四组 | [120,125) | 100 | 0.5 |
| 第五组 | [125,130) | 120 | 0.6 |
| 第六组 | [130,135) | 195 | y |
(Ⅱ)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取9份进行展出,并从9份试卷中选出两份作为优秀试卷,优秀试卷在[115,120)中的分数记为ξ,求随机变量ξ的分布列及期望.
15.已知抛物线y2=4x,过焦点F作直线与抛物线交于点A,B(点A在x轴下方),点A1与点A关于x轴对称,若直线AB斜率为1,则直线A1B的斜率为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
