题目内容
10.数列{an}中,若${a_1}=1,{a_{n+1}}=\frac{n}{n+1}{a_n}$,则an=$\frac{1}{n}$.分析 利用数列的递推关系式,通过累积法,求解数列的通项公式即可.
解答 解:数列{an}中,若${a_1}=1,{a_{n+1}}=\frac{n}{n+1}{a_n}$,
可得$\frac{{a}_{n}}{{a}_{n-1}}=\frac{n-1}{n}$,
可得:$\frac{{a}_{2}}{{a}_{1}}=\frac{1}{2}$,
$\frac{{a}_{3}}{{a}_{2}}$=$\frac{2}{3}$,
$\frac{{a}_{4}}{{a}_{3}}$=$\frac{3}{4}$,
…
得$\frac{{a}_{n}}{{a}_{n-1}}=\frac{n-1}{n}$,
累积可得
an=$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×…×\frac{n-1}{n}•{a}_{1}$=$\frac{1}{n}$.
故答案为:$\frac{1}{n}$.
点评 本题考查数列的递推关系式的应用,通项公式的求法,考查计算能力.

练习册系列答案
相关题目
4.两个函数的图象经过平移后能够重合,称这两个函数为“同形”函数,则下列四个函数:f1(x)=2log2(x+2),f2(x)=log2(x+2),f3(x)=log2(x+2)2,f4(x)=log22x,为“同形”函数的是( )
| A. | f1(x)与f3(x) | B. | f2(x)与f4(x) | C. | f1(x)与f2(x) | D. | f3(x)与f4(x) |
5.经过点(2,0)且与曲线$y=\frac{1}{x}$相切的直线方程为( )
| A. | x+4y+2=0 | B. | x+4y-2=0 | C. | x+y+2=0 | D. | x+y-2=0 |
15.设集合M={α|α=k•90°-36°,k∈Z},N={α|-180°<α<180°},则M∩N=( )
| A. | {-36°,54°} | B. | {-126°,144°} | ||
| C. | {-36°,54°,-126°,144°} | D. | {54°,-126°} |
2.曲线f(x)=ex在点(1,f(1))处的切线与该曲线及y轴围成的封闭图形的面积为( )
| A. | $\frac{e}{2}$ | B. | e | C. | e-1 | D. | $\frac{e}{2}$-1 |
20.调查表明:甲种农作物的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为x,y,z,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标ω=x+y+z的值评定这种农作物的长势等级,若ω≥4,则长势为一级;若2≤ω≤3,则长势为二级;若0≤ω≤1,则长势为三级,为了了解目前这种农作物长势情况,研究人员随机抽取10块种植地,得到如表中结果:
(Ⅰ)在这10块该农作物的种植地中任取两块地,求这两块地的空气湿度的指标z相同的概率;
(Ⅱ)从长势等级是一级的种植地中任取一块地,其综合指标为A,从长势等级不是一级的种植地中任取一块地,其综合指标为B,记随机变量X=A-B,求X的分布列及其数学期望.
| 种植地编号 | A1 | A2 | A3 | A4 | A5 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,0,1) | (1,2,1) |
| 种植地编号 | A6 | A7 | A8 | A9 | A10 |
| (x,y,z) | (1,1,2) | (1,1,1) | (1,2,2) | (1,2,1) | (1,1,1) |
(Ⅱ)从长势等级是一级的种植地中任取一块地,其综合指标为A,从长势等级不是一级的种植地中任取一块地,其综合指标为B,记随机变量X=A-B,求X的分布列及其数学期望.
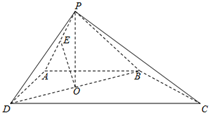 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的一动点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的一动点.