题目内容
13.若-2≤x≤2,则函数$f(x)={(\frac{1}{4})}^{x}-3•{(\frac{1}{2})}^{x}+2$的值域为[$-\frac{1}{4}$,6].分析 先写出$f(x)=(\frac{1}{2})^{2x}-3•(\frac{1}{2})^{x}+2$,从而可设$(\frac{1}{2})^{x}=t$,根据x的范围即可求出t的范围,进而得到二次函数y=t2-3t+2,这样配方求该函数的值域即可得出f(x)的值域.
解答 解:$f(x)=(\frac{1}{2})^{2x}-3•(\frac{1}{2})^{x}+2$,-2≤x≤2;
设$(\frac{1}{2})^{x}=t$,则$\frac{1}{4}≤t≤4$;
∴$y={t}^{2}-3t+2=(t-\frac{3}{2})^{2}-\frac{1}{4}$;
∴$t=\frac{3}{2}$时,${y}_{min}=-\frac{1}{4}$,t=4时,ymax=6;
∴f(x)的值域为$[-\frac{1}{4},6]$.
故答案为:$[-\frac{1}{4},6]$.
点评 考查指数式的运算,换元法求函数的值域,以及配方求二次函数值域的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知函数f(x)=cosx+ex-2(x<0)与g(x)=cosx+ln(x+m)图象上存在关于y轴对称的点,则m的取值范围是( )
| A. | (-∞,$\frac{1}{e}$) | B. | (-∞,$\frac{1}{\sqrt{e}}$) | C. | (-∞,$\sqrt{e}$) | D. | (-∞,e) |
5.经过点(2,0)且与曲线$y=\frac{1}{x}$相切的直线方程为( )
| A. | x+4y+2=0 | B. | x+4y-2=0 | C. | x+y+2=0 | D. | x+y-2=0 |
2.曲线f(x)=ex在点(1,f(1))处的切线与该曲线及y轴围成的封闭图形的面积为( )
| A. | $\frac{e}{2}$ | B. | e | C. | e-1 | D. | $\frac{e}{2}$-1 |
3.已知命题p:若$?x∈(-\frac{π}{2},0)$,tanx<0,命题q:?x0∈(0,+∞),${2^{x_0}}=\frac{1}{2}$,则下列命题为真命题的是
( )
( )
| A. | p∧q | B. | (¬p)∧(?q) | C. | p∧(¬q) | D. | (¬p)∧q |
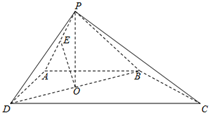 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的一动点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的一动点.