题目内容
9.在极坐标系中,O为极点,已知圆C的圆心$C(3,\frac{π}{6})$,半径r=3.(1)求圆C的极坐标方程;
(2)若点Q在圆C上运动,P在OQ的延长线上,且|OQ|:|QP|=3:2,求动点P的轨迹方程.
分析 (1)设M(ρ,θ)为圆C上任一点,OM的中点为N,由垂径定理能求出圆C的极坐标方程.
(2)设点P的极坐标为(ρ,θ),由已知求出点Q的极坐标为($\frac{3}{5}ρ$,θ),由此能求出点P的轨迹方程.
解答 解:(1)设M(ρ,θ)为圆C上任一点,OM的中点为N,
∵O在圆C上,∴△OCM为等腰三角形,由垂径定理得|ON|=|OC|cos($θ-\frac{π}{6}$),
∴|OM|=2×3cos($θ-\frac{π}{6}$),即ρ=6cos($θ-\frac{π}{6}$)为所求圆C的极坐标方程.(5分)
(2)设点P的极坐标为(ρ,θ),
∵P在OQ的延长线上,且|OQ|:|QP|=3:2,
∴点Q的极坐标为($\frac{3}{5}ρ$,θ),由于点Q在圆上,所以$\frac{3}{5}$ρ=6cos($θ-\frac{π}{6}$).
故点P的轨迹方程为ρ=10cos($θ-\frac{π}{6}$).(10分)
点评 本题考查圆的极坐标方程的求法,考查动点的轨迹方程的求法,是基础题,解题时要认真审题,注意极坐标和直角坐标互化公式的合理运用.

练习册系列答案
相关题目
20.下列各组中的两个函数是相等函数的是( )
| A. | y=x与y=$\frac{{x}^{2}}{x}$ | B. | y=($\sqrt{x}$)2-1与y=|x|-1 | C. | y=x2与y=$\root{3}{{x}^{6}}$ | D. | y=$\root{3}{{x}^{3}}与y=\sqrt{{x}^{2}}$ |
17.正方体ABCD-A1B1C1D1中,E,F,G分别在棱AB,CC1,D1A1上,且正方体的棱长为a,AE=CF=D1G=b,则DB1与平面EFG所成角为( )
| A. | 75° | B. | 60° | C. | 90° | D. | 15° |
14.函数f(x)=$\frac{1}{x}$-6+2x,x∈[1,+∞)的零点一定位于区间( )
| A. | (3,4) | B. | (2,3) | C. | (1,2) | D. | (5,6) |
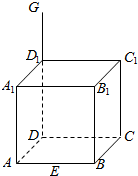 如图,G是正方体ABCD-A1B1C1D1的棱DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出过下列各点、直线的平面与正方体表面的交线.
如图,G是正方体ABCD-A1B1C1D1的棱DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出过下列各点、直线的平面与正方体表面的交线.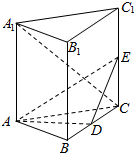 已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠ABC=$\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.
已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠ABC=$\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点. 如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.