题目内容
19.已知集合A={x|$\frac{2}{x-1}$<1},集合B={x|mx-1>0},若A∪B=A,则实数m的取值范围是m≤$\frac{1}{3}$.分析 由$\frac{2}{x-1}$<1,化为:$\frac{x-3}{x-1}$>0,即(x-1)(x-3)>0,可得:集合A={x|x<1或x>3},对于集合B={x|mx-1>0},对m分类讨论,利用A∪B=A即可得出.
解答 解:由$\frac{2}{x-1}$<1,化为:$\frac{x-3}{x-1}$>0,即(x-1)(x-3)>0,解得x>3,或x<1.∴集合A={x|x<1或x>3},
对于集合B={x|mx-1>0},当m=0时,B=∅,满足A∪B=A.
当m>0时,解得x$>\frac{1}{m}$,∵A∪B=A,∴$\frac{1}{m}$≥3,解得0<m≤$\frac{1}{3}$;
当m<0时,解得x$<\frac{1}{m}$,∵A∪B=A,∴$\frac{1}{m}$≤1,解得m<0.
综上可得:m≤$\frac{1}{3}$.
故答案为:m≤$\frac{1}{3}$.
点评 本题考查了不等式的解法、集合运算性质,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.定义在实数集R上的偶函数y=f(x)满足f(x+1)=f(1-x),且在区间[-1,0]上单调递增,设a=f(1),$b=f({\sqrt{2}})$,c=f(2),则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | a>c>b |
7.双曲线x2-4y2=4的渐近线方程是( )
| A. | y=±$\frac{1}{4}$x | B. | y=±$\frac{1}{2}$x | C. | y=±4x | D. | y=±2x |
14. 如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为( )
如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为( )
 如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为( )
如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.已知集合A={x|-1≤x≤1},B={x|x2-5x+6≥0},则下列结论中正确的是( )
| A. | A∩B=B | B. | A∪B=A | C. | A?B | D. | ∁RA=B |
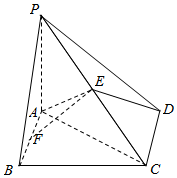 如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.
如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.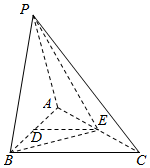 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.