题目内容
17.设x,y满足约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{2x+y≤2}\end{array}\right.$,目标函数z=ax+by(a>0,b>0)的最大值M,若M的取值范围是[1,2],则点M(a,b)所经过的区域面积=$\frac{3}{2}$.分析 作出可行域,变形目标函数,分类讨论不同情况下,M点对应的平面区域,相加可得答案.
解答 解:作出约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{2x+y≤2}\end{array}\right.$所对应的可行域(如图△OAB及内部),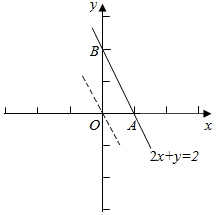
变形目标函数z=ax+by可得y=-$\frac{a}{b}$x+$\frac{1}{b}$z,
当-$\frac{a}{b}$≤-2时,直线经过点A(1,0)时,z取最大值a∈[1,2],
由$\left\{\begin{array}{l}a>0\\ b>0\\-\frac{a}{b}≤-2\\ a∈[1,2]\end{array}\right.$得点M(a,b)所经过的区域如下图所示: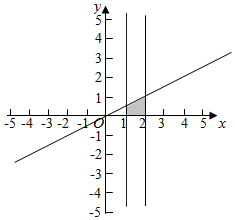
故点M(a,b)所经过的区域面积S=$\frac{3}{4}$,
当-$\frac{a}{b}$>-2时,直线经过点B(0,2)时,z取最大值2b∈[1,2],
由$\left\{\begin{array}{l}a>0\\ b>0\\-\frac{a}{b}≤-2\\ 2b∈[1,2]\end{array}\right.$得点M(a,b)所经过的区域如下图所示: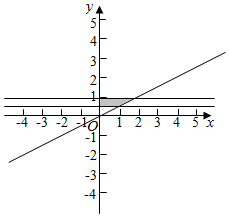
故点M(a,b)所经过的区域面积S=$\frac{3}{4}$,
综上可得:点M(a,b)所经过的区域面积面积S=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
相关题目
7.式子$\frac{m(m+1)(m+2)…(m+20)}{20!}$可表示为( )
| A. | A${\;}_{m+20}^{20}$ | B. | C${\;}_{m+20}^{20}$ | C. | 21C${\;}_{m+20}^{20}$ | D. | 21C${\;}_{m+20}^{21}$ |
8.若在曲线y=a2x+x+1(a>0,且a≠1)上的点(0,m)处的切线与直线mx-y+1=0平行,则m+a=( )
| A. | 1+e | B. | 1+$\sqrt{e}$ | C. | 2+e | D. | 2+$\sqrt{e}$ |
6.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点F向其一条渐近线作垂线l,垂足为A,l与另一条渐近线交于B点,若$\overrightarrow{FB}$=3$\overrightarrow{FA}$,则双曲线的离心率为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | 2 | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$ |

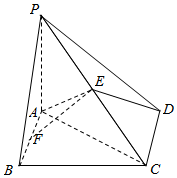 如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.
如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.