题目内容
13.数列{an}的通项公式为an=n2-kn,若对一切的n∈N*不等式an≥a3,则实数k的取值范围[5,7].分析 结合二次函数f(x)=x2-kx的性质可得$\frac{2+3}{2}$≤$\frac{k}{2}$≤$\frac{3+4}{2}$,从而求得.
解答 解:∵数列{an}的通项公式为an=n2-kn,
结合二次函数f(x)=x2-kx的性质,
又∵f(x)=x2-kx的图象的对称轴为x=$\frac{k}{2}$,
故对一切的n∈N*不等式an≥a3可化为
$\frac{2+3}{2}$≤$\frac{k}{2}$≤$\frac{3+4}{2}$,
即5≤k≤7,
故答案为:[5,7].
点评 本题考查了数列的性质的判断与应用,同时考查了函数的性质的判断与应用,属于中档题.

练习册系列答案
相关题目
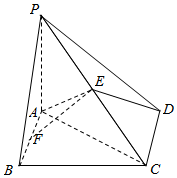 如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.
如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD. 如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,CD=BC=$\frac{1}{2}$AB=1,点P为CE中点.
如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,CD=BC=$\frac{1}{2}$AB=1,点P为CE中点.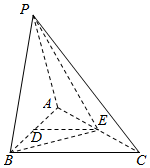 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.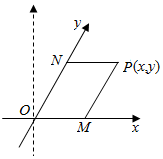 如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.
如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.