题目内容
15．以双曲线x2-$\frac{{y}^{2}}{2}$=1的左顶点为焦点的抛物线的标准方程为y2=-4x．分析 求得双曲线的左顶点坐标，设出抛物线的方程为y2=-2px（p＞0），求得焦点，解方程可得p=2，进而得到抛物线的方程．
解答 解：双曲线x2-$\frac{{y}^{2}}{2}$=1的左顶点为（-1，0），
可设抛物线的方程为y2=-2px（p＞0），
可得-$\frac{p}{2}$=-1，解得p=2，
则抛物线的方程为y2=-4x．
故答案为：y2=-4x．
点评 本题考查抛物线的标准方程的求法，注意运用双曲线的方程和性质，考查运算能力，属于基础题．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
8．若在曲线y=a2x+x+1（a＞0，且a≠1）上的点（0，m）处的切线与直线mx-y+1=0平行，则m+a=（ ）
| A． | 1+e | B． | 1+$\sqrt{e}$ | C． | 2+e | D． | 2+$\sqrt{e}$ |
6．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一个焦点F向其一条渐近线作垂线l，垂足为A，l与另一条渐近线交于B点，若$\overrightarrow{FB}$=3$\overrightarrow{FA}$，则双曲线的离心率为（ ）
| A． | $\frac{\sqrt{6}}{3}$ | B． | 2 | C． | $\frac{\sqrt{6}}{2}$ | D． | $\sqrt{3}$ |
10．定义在实数集R上的偶函数y=f（x）满足f（x+1）=f（1-x），且在区间[-1，0]上单调递增，设a=f（1），$b=f（{\sqrt{2}}）$，c=f（2），则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | c＞b＞a | C． | b＞c＞a | D． | a＞c＞b |
7．双曲线x2-4y2=4的渐近线方程是（ ）
| A． | y=±$\frac{1}{4}$x | B． | y=±$\frac{1}{2}$x | C． | y=±4x | D． | y=±2x |
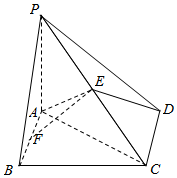如图，在四棱锥中P-ABCD，底面ABCD为边长为$\sqrt{2}$的正方形，PA⊥BD．
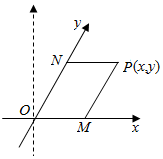如图，将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后，构成一个斜坐标平面xOy．在此斜坐标平面xOy中，点P（x，y）的坐标定义如下：过点P作两坐标轴的平行线，分别交两轴于M，N两点，则M在Ox轴上表示的数为x，N在Oy轴上表示的数为y．那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0．