题目内容
无论从左往右读,还是从右往左读,都是同一个数,称这样的数为“和谐数”,如:88,454,7337,43534等都是“和谐数”.
两位的“和谐数”有11,22,33,44,55,66,77,88,99,共9个;
三位的“和谐数”有101,111,121,131,…,969,979,989,999,共90个;
四位的“和谐数”有1001,1111,1221,…,9669,9779,9889,9999,共90个;
由此推测:六位的“和谐数”总共有 个.
两位的“和谐数”有11,22,33,44,55,66,77,88,99,共9个;
三位的“和谐数”有101,111,121,131,…,969,979,989,999,共90个;
四位的“和谐数”有1001,1111,1221,…,9669,9779,9889,9999,共90个;
由此推测:六位的“和谐数”总共有
考点:计数原理的应用
专题:排列组合
分析:根据新定义,可以判断各位数的情况,根据分步计数可得答案
解答:
解:根据“和谐数”的定义,“和谐数”的首位和末尾是相同的,故两位或两位以上的“和谐数”的末尾不能为0,故末尾和首位有9种选择,其余的有10种选择.
对于位数是偶数的“和谐数”,其中有一半位数确定了,这个数就确定了.
故有9×10×10=900 个,
故答案为:900.
对于位数是偶数的“和谐数”,其中有一半位数确定了,这个数就确定了.
故有9×10×10=900 个,
故答案为:900.
点评:本题主要考查排列、组合以及两个基本原理的应用,注意理解“和谐数”的定义和特点,属于中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
空间四边形ABCD中,若AD⊥BC,AD⊥BD,那么有( )
| A、平面ABC⊥平面ADC |
| B、平面ABC⊥平面ADB |
| C、平面ABC⊥平面DBC |
| D、平面ADC⊥平面DBC |
已知一个三棱柱的三视图如图所示,则该三棱柱的表面积为( )
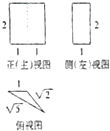

A、4
| ||||||
B、2
| ||||||
C、
| ||||||
D、2
|
设函数f(x)=
,g(x)=x2f(x-1),则函数g(x)的递减区间是( )
|
| A、(0,1] |
| B、(0,1) |
| C、(-∞,0) |
| D、(0,+∞) |