题目内容
17.已知点$F(0,\frac{1}{4})$是抛物线x2=2py(p>0)的焦点,设A(2,y0)是抛物线上的一点.(1)求该抛物线在点A处的切线l的方程;
(2)求曲线C、直线l和x轴所围成的图形的面积.
分析 (1)由题意,抛物线的方程为x2=y,A(2,4),求出切线斜率,可得该抛物线在点A处的切线l的方程;
(2)利用定积分求曲线C、直线l和x轴所围成的图形的面积.
解答 解:(1)由题意,抛物线的方程为x2=y,A(2,4),
∵y=x2,∴y′=2x,
∴x=2时,y′=4,
∴该抛物线在点A处的切线l的方程为y-4=4(x-2),即4x-y-4=0;
(2)曲线C、直线l和x轴所围成的图形的面积S=${∫}_{0}^{2}({x}^{2}-4x+4)dx$=($\frac{1}{3}{x}^{3}-2{x}^{2}+4x$)${|}_{0}^{2}$=$\frac{8}{3}$.
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查定积分求面积,属于中档题.

练习册系列答案
相关题目
8.已知椭圆的中心在原点,离心率e=$\frac{1}{2}$,且它的一个焦点与抛物线x2=-4y的焦点重合,则此椭圆的方程为( )
| A. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$ | B. | $\frac{{x}^{2}}{3}+\frac{{y}^{2}}{4}=1$ | C. | ${x}^{2}+\frac{{y}^{2}}{2}=1$ | D. | $\frac{{x}^{2}}{6}+\frac{{y}^{2}}{8}=1$ |
9.现有如下的错误推理:“因为任何复数的平方都大于等于0,而i是复数,所以i2>0,即-1>0”,其错误的原因是( )
| A. | 大前提错误导致结论错误 | B. | 小前提错误导致结论错误 | ||
| C. | 推理形式错误导致结论错误 | D. | 大前提和推理形式都错误导致错误 |
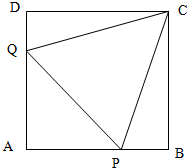 如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且都不与A,B,D重合,线段PQ的长为1,△CPQ的面积用y表示.
如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且都不与A,B,D重合,线段PQ的长为1,△CPQ的面积用y表示.