题目内容
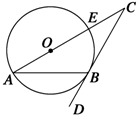如图所示，CD切⊙O于B，CO的延长线交⊙O于A，若∠C=36°，则∠ABD的度数是（ ）| A、72° | B、63° |
| C、54° | D、36° |
考点：弦切角
专题：直线与圆,立体几何
分析：连结OB，则∠OBC=90°．由已知条件求出∠A=27°．由此能求出∠ABD的度数．
解答：
解：连结OB．∵CD为⊙O的切线，∴∠OBC=90°．
∵∠C=36°，∴∠BOC=54°．
又∵∠BOC=2∠A，∴∠A=27°．
∴∠ABD=∠A+∠C=27°+36°=63°．
故选：B．
∵∠C=36°，∴∠BOC=54°．
又∵∠BOC=2∠A，∴∠A=27°．
∴∠ABD=∠A+∠C=27°+36°=63°．
故选：B．
点评：本题考查角的大小的求法，是基础题，解题时要认真审题，注意切线性质的灵活运用．
练习册系列答案
相关题目
把正整数按一定的规则排成了如图所示的三角形数表，设aij（i，j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右第j个数，如a42=8．若aij=26，则（i，j）=极点到极坐标方程ρsin(θ+
)=
的距离是（ ）
| π |
| 3 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在三角形ABC中，c=5，b=3，a=7，则角A的大小为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设x，y∈R，则“x≥2，且y≥2”是“x2+y2≥8”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知sinθ＞0，cosθ＜0，则θ为（ ）
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
已知F为抛物线x2=2py（p＞0）的焦点，M为其上一点，且|MF|=2p，则直线MF的斜率为（ ）
A、-
| ||||
B、±
| ||||
C、-
| ||||
D、±
|
已知sinαcosα=
，且π＜α＜
，则cosα-sinα的值为（ ）
| 1 |
| 8 |
| 5π |
| 4 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|