题目内容
已知sinθ＞0，cosθ＜0，则θ为（ ）
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
考点：三角函数值的符号
专题：三角函数的求值
分析：利用三角函数值的符号与象限角的关系即可得出．
解答：
解：∵sinθ＞0，cosθ＜0，∴θ为第二象限角．
故选：B．
故选：B．
点评：本题考查了三角函数值的符号与象限角的关系，属于基础题．
练习册系列答案
发散思维新课堂系列答案
相关题目
12个篮球队中有3个强队，任意分成三个组（每组4个队），则3个强队恰好被分在同一组的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
对于回归分析，下列说法错误的是（ ）
| A、在回归分析中，变量间的关系若是非确定关系，那么因变量不能由自变量唯一确定 |
| B、样本相关系数r∈（-1，1） |
| C、回归分析中，如果r2=1，说明x与y之间完全相关 |
| D、线性相关系数可以是正的，也可以是负的 |
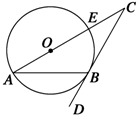如图所示，CD切⊙O于B，CO的延长线交⊙O于A，若∠C=36°，则∠ABD的度数是（ ）| A、72° | B、63° |
| C、54° | D、36° |
若向量
=（1，λ，2），
=（2，-1，2），cos＜
，
＞=
，则λ的值为（ ）
| a |
| b |
| a |
| b |
| 8 |
| 9 |
| A、-2 | ||
B、
| ||
C、-2或
| ||
| D、2 |
下列关于函数f（x）=sin（2x+
）的结论：
①f（x）的最小正周期是2π；
②f（x）在区间[kπ-
，kπ+
]（k∈Z）上单调递增；
③当x∈[0，
]时，f（x）的值域为[-
，
]；
④函数y=f（x+
）是偶函数．
其中正确的结论为（ ）
| π |
| 3 |
①f（x）的最小正周期是2π；
②f（x）在区间[kπ-
| 5π |
| 12 |
| π |
| 12 |
③当x∈[0，
| π |
| 2 |
| ||
| 2 |
| ||
| 2 |
④函数y=f（x+
| π |
| 12 |
其中正确的结论为（ ）
| A、①② | B、②③ | C、②④ | D、③④ |
点P（-1，1）关于直线ax-y+b=0的对称点是Q（3，-1），则a、b的值依次是（ ）
| A、-2，2 | ||||
| B、2，-2 | ||||
C、
| ||||
D、-
|
阅读如图所示的程序框图．若输入m=8，n=6，则输出的a，i分别等于（ ）| A、12，2 | B、12，3 |
| C、24，2 | D、24，3 |