题目内容
 把正整数按一定的规则排成了如图所示的三角形数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右第j个数,如a42=8.若aij=26,则(i,j)=
把正整数按一定的规则排成了如图所示的三角形数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右第j个数,如a42=8.若aij=26,则(i,j)=考点:等差数列的性质,归纳推理
专题:等差数列与等比数列
分析:由三角形数表可以看出其奇数行为奇数列,偶数行为偶数列,26为第13个偶数,前31个偶数行中数的个数为992个,由此入手能得到结果.
解答:
解:由三角形数表可以看出其奇数行为奇数列,偶数行为偶数列,
∵26=2×13,
∴26为第13个偶数,
又∵前3个偶数行内数的个数和为12,
∴26为第四个偶数行的第1个数,
∴a81=26,∴(i,j)=(8,1).
∵2014=1012×2,
∴2014是第1012个数,
∵前31个偶数行中数的个数为992个,
∵第32行的第一个数是992×2=1984,
∴2014=1984+(j-1)×2,解得j=15.
∴i=32×2=64,j=15,
∴i+j=79.
故答案为:(8,1),79.
∵26=2×13,
∴26为第13个偶数,
又∵前3个偶数行内数的个数和为12,
∴26为第四个偶数行的第1个数,
∴a81=26,∴(i,j)=(8,1).
∵2014=1012×2,
∴2014是第1012个数,
∵前31个偶数行中数的个数为992个,
∵第32行的第一个数是992×2=1984,
∴2014=1984+(j-1)×2,解得j=15.
∴i=32×2=64,j=15,
∴i+j=79.
故答案为:(8,1),79.
点评:本题考查简单的演绎推理,考查数列的特点,是一个综合题,这种题目是我们经常见到的问题,是一个比较新颖的题目,注意观察分析数字的排列规律.

练习册系列答案
相关题目
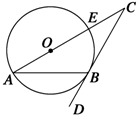 如图所示,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是( )
如图所示,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是( )| A、72° | B、63° |
| C、54° | D、36° |
