题目内容
已知函数f(x)=
,(a>0且a≠1).
(1)求函数f(x)的定义域和值域.
(2)判断f(x)与f(-x)的关系.
(3)讨论函数f(x)的单调性.
| ax-1 |
| ax+1 |
(1)求函数f(x)的定义域和值域.
(2)判断f(x)与f(-x)的关系.
(3)讨论函数f(x)的单调性.
考点:指数函数综合题
专题:函数的性质及应用
分析:(1)根据ax>0,可得函数的定义域为R,再根据 ax=
>0,求得y的范围,可得函数的值域.
(2)化简f(-x) 的解析式,可得它与-f(x)的关系.
(3)根据 f(x)=
=1-
,再分当a>1时 和当0<a<1时 两种情况,分别根据函数
的单调性,求得f(x)的单调性.
| 1+y |
| 1-y |
(2)化简f(-x) 的解析式,可得它与-f(x)的关系.
(3)根据 f(x)=
| ax+1-2 |
| ax+1 |
| 2 |
| ax+1 |
| 2 |
| ax+1 |
解答:
解:(1)∵函数f(x)=
,(a>0且a≠1),ax>0,∴函数的定义域为R,
再根据 ax=
>0,求得-1<y<1,故函数的值域为(-1,1).
(2)f(-x)=f(x)=
=
=-
=-f(x).
(3)∵f(x)=
=1-
,
当a>1时,由于函数
是减函数,故f(x)为增函数;
当0<a<1时,由于函数
是增函数,故f(x)为减函数.
| ax-1 |
| ax+1 |
再根据 ax=
| 1+y |
| 1-y |
(2)f(-x)=f(x)=
| a-x-1 |
| a-x+1 |
| 1-ax |
| 1+ax |
| ax-1 |
| ax+1 |
(3)∵f(x)=
| ax+1-2 |
| ax+1 |
| 2 |
| ax+1 |
当a>1时,由于函数
| 2 |
| ax+1 |
当0<a<1时,由于函数
| 2 |
| ax+1 |
点评:本题主要考查求函数的定义域和值域,函数的单调性的判断和证明,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
若x2+y2=100,则直线4x-3y+50=0与圆的位置关系是( )
| A、相交 | B、相离 |
| C、相切 | D、相交但不过圆心 |
已知a,b,c∈R,给出下列命题:
①若a>b,则ac2>bc2;
②若ab≠0,则
+
≥2;
③若a>b>0,n∈N*,则an>bn;
④若logab<0(a>0,a≠1),则a,b中至少有一个大于1.
其中真命题的个数为( )
①若a>b,则ac2>bc2;
②若ab≠0,则
| a |
| b |
| b |
| a |
③若a>b>0,n∈N*,则an>bn;
④若logab<0(a>0,a≠1),则a,b中至少有一个大于1.
其中真命题的个数为( )
| A、2 | B、3 | C、4 | D、1 |
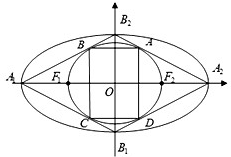 如图,椭圆
如图,椭圆