题目内容
下列函数中,在区间(1,+∞)上是增函数的是( )
A、y=
| ||
| B、y=-x+1 | ||
C、y=log
| ||
| D、y=x2-2x+3 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据反比例函数,一次函数,对数函数,二次函数的单调性,分析四个答案中的函数在区间(1,+∞)上单调性,进而可得答案.
解答:
解:A中,函数y=
在区间(1,+∞)上是减函数,不满足要求;
B中,函数y=-x+1在区间(1,+∞)上是减函数,不满足要求;
C中,函数y=log
x在区间(1,+∞)上是减函数,不满足要求;
D中,函数y=x2-2x+3在区间(1,+∞)上是增函数,满足要求;
故选:D
| 1 |
| x |
B中,函数y=-x+1在区间(1,+∞)上是减函数,不满足要求;
C中,函数y=log
| 1 |
| 2 |
D中,函数y=x2-2x+3在区间(1,+∞)上是增函数,满足要求;
故选:D
点评:本题考查的知识点是函数单调性的判断与证明,熟练掌握各种基本初等函数的单调性,是解答的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
对于任意实数a、b、c、d,下列命题:
①若a>b,c≠0,则ac>bc;
②若a>b,则ac2>bc2;
③若ac2>bc2,则a>b;
④若a>b,则
<
中.
真命题个数为( )
①若a>b,c≠0,则ac>bc;
②若a>b,则ac2>bc2;
③若ac2>bc2,则a>b;
④若a>b,则
| 1 |
| a |
| 1 |
| b |
真命题个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知P=(x2+1)2,Q=x4+x2+1,那么P,Q的大小关系是( )
| A、P≥Q | B、P<Q |
| C、P≤Q | D、无法确定 |
给出下列三个命题:
①有四个相邻侧面互相垂直的棱柱是直棱柱;
②各侧面都是正方形的四棱柱是正方体;
③底面是正三角形,各侧面都是等腰三角形的三棱锥是正三棱锥.
其中真命题的个数是( )
①有四个相邻侧面互相垂直的棱柱是直棱柱;
②各侧面都是正方形的四棱柱是正方体;
③底面是正三角形,各侧面都是等腰三角形的三棱锥是正三棱锥.
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、0 |
对于原命题:“单调函数不是周期函数”,下列陈述正确的是 ( )
| A、逆命题为“周期函数不是单调函数” |
| B、否命题为“单调函数是周期函数” |
| C、逆否命题为“周期函数是单调函数” |
| D、以上三者都不正确 |
图中最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得.现用一个竖直的平面去截这个几何体,则截面图形可能是( )

| A、(1)(2) |
| B、(1)(3) |
| C、(1)(4) |
| D、(1)(5) |
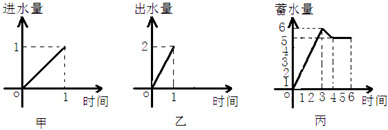 一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:
一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断: