题目内容

17．设等差数列{an}的前n项和为Sn，已知a4+a6=-6，则S9=（　　）
A．-27B．27C．-54D．54

分析 由等差数列{an}的性质可得：a4+a6=-6=a1+a9，再利用等差数列的前n项和公式即可得出．

解答 解：由等差数列{an}的性质可得：a4+a6=-6=a1+a9，
则S9=$\frac{9（{a}_{1}+{a}_{9}）}{2}$=9×（-3）=-27．
故选：A．

点评 本题考查了等差数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
7．已知集合A={x|0＜log4x＜1}，B={x|x2-4≤0}，则A∩B=（　　）
A．（0，1）B．（0，2]C．（1，2）D．（1，2]
8．如果数据x1，x2，…，xn的平均数为2，方差为3，则数据3x1+5，3x2+5…，3xn+5的平均数和方差分别为（　　）
A．11，25B．11，27C．8，27D．11，8
5．已知集合A={1，2}，B={0，1}，则集合A∪B的所有子集的个数为8个．
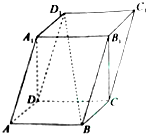12．已知四棱柱ABCD-A1B1C1D1，侧面A1ADD1⊥面ABCD，底面ABCD是矩形，且AB=2，AD=1，AA1=$\sqrt{5}$，∠A1AD的余弦值为$\frac{\sqrt{5}}{5}$．
（1）求证：平面A1DCB1⊥平面ABCD；
（2）求BD1与平面ABCD所成角的正切值．
2．已知命题p：?x0∈R，使x0+$\frac{1}{3}$m=${e^{x_0}}$；（e是自然对数的底数），命题q：椭圆$\frac{x^2}{m}+\frac{y^2}{5}$=1的离心率的范围是$（{\frac{1}{2}，\frac{2}{3}}）$．若（?p）∨（?q）为假命题，求实数m的取值范围．
9．在数列{an}中，a1=1，a2=5，an+2=an+1-an（n∈N*），则a1000=-1．
6．已知函数f（x）=lg$\frac{2x}{ax+b}$，f（1）=0，且f（2）-f（$\frac{1}{2}$）=lg2．
（1）求f（x）的表达式；
（2）若x∈（0，+∞）时方程f（x）=lgt有解，求实数t的取值范围；
（3）若函数y=f（x）-lg（8x+m）的无零点，求实数m的取值范围．
7．已知数列{an}满足：a1=1，an+1=$\frac{n{a}_{n}^{2}}{n+1}$，n∈N*．
（Ⅰ）证明：
（i）an+1＜an≤1；
（ii）an≤$\frac{1}{n}$；
（Ⅱ）证明：a1+a2+…+an＜$\frac{7}{4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网