题目内容
已知数列{an}满足a1=1,an-2an-1-2n-1=0(n∈N*,n≥2).
(1)求证:数列{
}是等差数列;
(2)若数列{an}的前n项和为Sn,求Sn.
(1)求证:数列{
| an |
| 2n |
(2)若数列{an}的前n项和为Sn,求Sn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件推导出
-
=
,由此证明{
}是以
为首项,
为公比的等差数列.
(2)由(1)知
=
+
(n-1),从而得到an=n•2n-1,由此利用错位相减法能求出数列{an}的前n项和Sn.
| an |
| 2n |
| an-1 |
| 2n-1 |
| 1 |
| 2 |
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)知
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
(1)证明:∵数列{an}满足a1=1, an-2an-1-2n-1=0(n∈N*,n≥2),
∴
-
=
,
又
=
,
∴{
}是以
为首项,
为公比的等差数列.
(2)解:由(1)知
=
+
(n-1),
∴an=n•2n-1,
∴Sn=1•20+2•2+3•22+…+n•2n-1,①
2Sn=1•2+2•22+3•23+…+n•2n,②
①-②,得:
-Sn=1=1+2+22+…+2n-n•2n
=
-n•2n
=2n-1-n•2n,
∴Sn=(n-1)•2n+1.
∴
| an |
| 2n |
| an-1 |
| 2n-1 |
| 1 |
| 2 |
又
| a1 |
| 2 |
| 1 |
| 2 |
∴{
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
(2)解:由(1)知
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
∴an=n•2n-1,
∴Sn=1•20+2•2+3•22+…+n•2n-1,①
2Sn=1•2+2•22+3•23+…+n•2n,②
①-②,得:
-Sn=1=1+2+22+…+2n-n•2n
=
| 1-2n |
| 1-2 |
=2n-1-n•2n,
∴Sn=(n-1)•2n+1.
点评:本题考查等差数列的证明,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
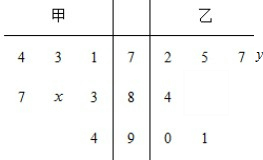 某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某一班的7名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班7名学生成绩的平均分是81,乙班7名学生成绩的中位数是78.
某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某一班的7名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班7名学生成绩的平均分是81,乙班7名学生成绩的中位数是78. 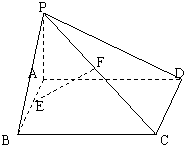 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点. 在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“折线路径”,所有“折线路径”中长度最小的称为M到N的“折线距离”.如图所示的路径MD1D2D3N与路径MEN都是M到N的“折线路径”.某地有三个居民区分别位于平面xOy内三点A(-8,1),B(5,2),C(1,14),现计划在这个平面上某一点P(x,y)处修建一个超市.
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“折线路径”,所有“折线路径”中长度最小的称为M到N的“折线距离”.如图所示的路径MD1D2D3N与路径MEN都是M到N的“折线路径”.某地有三个居民区分别位于平面xOy内三点A(-8,1),B(5,2),C(1,14),现计划在这个平面上某一点P(x,y)处修建一个超市.