题目内容
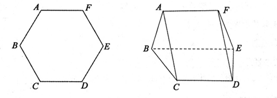
如图,将边长为2的正六边形ABDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且AC=
.
(1)证明:平面ABEF⊥平面BCDE;
(2)求三棱锥E-ABC的体积.
| 6 |
(1)证明:平面ABEF⊥平面BCDE;
(2)求三棱锥E-ABC的体积.

考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)连结AC、BE,交点为G,由边长为2的正六边形ABCDEF的性质得AC⊥BE,且AG=CG=
,由勾股定理得AG⊥GC,从而AG⊥平面BCDE,由此能证明平面ABEF⊥平面BCDE.
(2)连结AE,CE,则AG为三棱锥A-BCE的高,GC为△BCE的高,利用VE-ABC=VA-BCE,能求出三棱锥E-ABC的体积.
| 3 |
(2)连结AE,CE,则AG为三棱锥A-BCE的高,GC为△BCE的高,利用VE-ABC=VA-BCE,能求出三棱锥E-ABC的体积.
解答:
(1)证明:正六边形ABCDEF中,连结AC、BE,交点为G,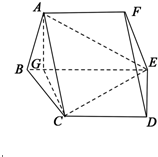
由边长为2的正六边形ABCDEF的性质得AC⊥BE,且AG=CG=
,
在多面体中,由AC=
,得AG2+CG2=AC2,
∴AG⊥GC,
又GC∩BE=G,GC,BE?平面BCDE,
∴AG⊥平面BCDE,
又AG?平面ABEF,∴平面ABEF⊥平面BCDE.
(2)解:连结AE,CE,则AG为三棱锥A-BCE的高,GC为△BCE的高,
在正六边形ABCDEF中,BE=2AF=4,
∴S△BCE=
×4×
=2
,
∴VE-ABC=VA-BCE=
×2
×
=2.

由边长为2的正六边形ABCDEF的性质得AC⊥BE,且AG=CG=
| 3 |
在多面体中,由AC=
| 6 |
∴AG⊥GC,
又GC∩BE=G,GC,BE?平面BCDE,
∴AG⊥平面BCDE,
又AG?平面ABEF,∴平面ABEF⊥平面BCDE.
(2)解:连结AE,CE,则AG为三棱锥A-BCE的高,GC为△BCE的高,
在正六边形ABCDEF中,BE=2AF=4,
∴S△BCE=
| 1 |
| 2 |
| 3 |
| 3 |
∴VE-ABC=VA-BCE=
| 1 |
| 3 |
| 3 |
| 3 |
点评:本小题主要考查空间线面关系、面面垂直的证明、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若曲线y=x2+ax+b在点(1,1)处的切线为3x-y-2=0,则有( )
| A、a=-1,b=1 |
| B、a=-1,b=-1 |
| C、a=-2,b=1 |
| D、a=2,b=-1 |
在区间[0,π]上随机取一个数x,则事件“sinx+cosx≥
”发生的概率为( )
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,正方体ABCD-A1B1C1D1的棱长为1,E为棱DD1上的点,F为AB的中点,则三棱锥B1-BFE的体积为
如图,正方体ABCD-A1B1C1D1的棱长为1,E为棱DD1上的点,F为AB的中点,则三棱锥B1-BFE的体积为 如图是某几何体的三视图,试求它的体积(单位:cm).
如图是某几何体的三视图,试求它的体积(单位:cm).