题目内容
已知点Q为圆C:x2+(y-2)2=9上的一点,P是Q关于直线l:y=2(x-4)的对称点,求动点P的轨迹方程.
考点:轨迹方程
专题:计算题,直线与圆
分析:由Q与P关于直线L:y=2x-8对称可知,P的轨迹也是半径等于3的圆,求出圆心的坐标,即可得出结论.
解答:
解:x2+(y-2)2=9,这是圆心在(0,2),半径等于3的圆
由Q与P关于直线l:y=2(x-4)对称可知,P的轨迹也是半径等于3的圆,
而其圆心(a,b)与圆C的圆心关于y=2(x-4)对称,
∴
,解得a=8,b=-2
故P的轨迹方程为 (x-8)2+(y+2)2=9.
由Q与P关于直线l:y=2(x-4)对称可知,P的轨迹也是半径等于3的圆,
而其圆心(a,b)与圆C的圆心关于y=2(x-4)对称,
∴
|
故P的轨迹方程为 (x-8)2+(y+2)2=9.
点评:本题考查轨迹方程,考查对称点的求法,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
空间中有四点A,B,C,D,其中
=(2m,m,2),
=(m,m+1,-5),且
+
=(5,
,-3),则直线AB和CD( )
| AB |
| CD |
| AB |
| CD |
| 13 |
| 3 |
| A、平行 | B、异面 |
| C、必定相交 | D、必定垂直 |
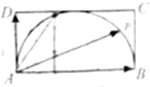 如图,矩形ABCD中,AB=2AD=2,点P在以AB为直径的半圆上移动,若
如图,矩形ABCD中,AB=2AD=2,点P在以AB为直径的半圆上移动,若| AP |
| AB |
| AD |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
若曲线y=x2+ax+b在点(1,1)处的切线为3x-y-2=0,则有( )
| A、a=-1,b=1 |
| B、a=-1,b=-1 |
| C、a=-2,b=1 |
| D、a=2,b=-1 |
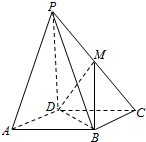 在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是边长为2的正方形,且PD=AB.
在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是边长为2的正方形,且PD=AB. 如图,正方体ABCD-A1B1C1D1的棱长为1,E为棱DD1上的点,F为AB的中点,则三棱锥B1-BFE的体积为
如图,正方体ABCD-A1B1C1D1的棱长为1,E为棱DD1上的点,F为AB的中点,则三棱锥B1-BFE的体积为 如图是某几何体的三视图,试求它的体积(单位:cm).
如图是某几何体的三视图,试求它的体积(单位:cm).