题目内容
对于z=(
)100+(
)200,下列结论成立的是( )
| 1+i | ||
|
| 1-i | ||
|
| A、z是零 | B、z是纯虚数 |
| C、z是正实数 | D、z是负实数 |
考点:复数代数形式的混合运算
专题:数系的扩充和复数
分析:先计算(
)2=
=i,(
)2=
=-i,再利用复数的运算法则即可得出.
| 1+i | ||
|
| 2i |
| 2 |
| 1-i | ||
|
| -2i |
| 2 |
解答:
解:∵(
)2=
=i,(
)2=
=-i,
∴z=(
)100+(
)200=i50+(-i)50=-1-1=-2.
故选:D.
| 1+i | ||
|
| 2i |
| 2 |
| 1-i | ||
|
| -2i |
| 2 |
∴z=(
| 1+i | ||
|
| 1-i | ||
|
故选:D.
点评:本题考查了复数的运算法则,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
用数学归纳法证明2n>n2(n∈N*,n≥5)成立时,第二步归纳假设正确写法( )
| A、假设n=k时命题成立 |
| B、假设n=k(k∈N*)时命题成立 |
| C、假设n=k(n≥5)时命题成立 |
| D、假设n=k(n>5)时命题成立 |
若函数f(x)=
(a,b,c,d∈R)的图象如图所示,则a:b:c:d=( )
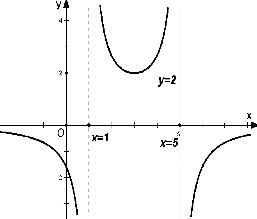
| d |
| ax2+bx+c |

| A、1:6:5:8 |
| B、1:6:5:(-8) |
| C、1:(-6):5:8 |
| D、1:(-6):5:(-8) |
已知y=
x3+bx2+(b+2)x+3在R上是增函数,则b的取值范围为( )
| 1 |
| 3 |
| A、(-1,2) |
| B、[-1,2] |
| C、(-2,1) |
| D、[-2,1] |
已知数列{an}的前n项和为Sn,且Sn=n2+2n+1,则a3+a4+a5=( )
| A、11 | B、16 | C、27 | D、32 |
已知等差数列{an}的前n项和为Sn,且a3+a5+2a10=4,则S13的值为( )
| A、13 | B、26 | C、8 | D、162 |
独立性检验,适用于检查( )变量之间的关系.
| A、线性 | B、非线性 |
| C、解释与预报 | D、分类 |
不等式x2-3x-10<0的解集为( )
| A、{x|2<x<5} |
| B、{x|-5<x<2} |
| C、{x|-2<x<5} |
| D、{x|-5<x<-2} |