题目内容
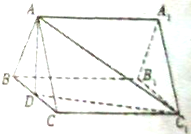如图，在三棱柱ABC-A1B1C1中，底面ABC是边长为2的正三角形，侧棱长为2，且侧棱AA1⊥底面ABC，点D是BC的中点（1）求证：AD⊥C1D；
（2）求直线AC与平面ADC1所成角的余弦值．
考点：直线与平面所成的角
专题：空间位置关系与距离
分析：（1）由题设条件推导出AD⊥平面BCC1B1，由此能够AD⊥C1D．
（2）过点C作CO⊥C1D，交C1D于点O．连结AO，∠ACO是直线AC与平面ADC1所成角，由此能求出AC与平面ADC1所成角的余弦值．
（2）过点C作CO⊥C1D，交C1D于点O．连结AO，∠ACO是直线AC与平面ADC1所成角，由此能求出AC与平面ADC1所成角的余弦值．
解答：
解：（1）∵三棱柱ABC-A1B1C1是正三棱柱，
∴C1C⊥平面ABC，
又∵AD?平面ABC，∴C1C⊥AD，…（2分）
又点D是棱BC的中点，
且△ABC为正三角形，∴AD⊥BC，
∵BC∩C1C=C，∴AD⊥平面BCC1B1，…（4分）
又∵DC1?平面BCC1B1，∴AD⊥C1D．…（6分）
（2）过点C作CO⊥C1D，交C1D于点O．连结AO，
∵AD⊥平面BCC1B1，CO?平面BCC1B1，
∴CO⊥平面ADC1，…（8分）
∴∠ACO是直线AC与平面ADC1所成角，…（9分）
又∵∠COD=∠DCC1=90°，
∠ODC=∠ODC，
∴△ODC∽△DCC1．…（10分）
∵底面ABC是边长为2的正三角形，侧棱长为2，
且侧棱AA1⊥底面ABC，点D是BC的中点
∴DC=1，CC1=2，DC1=
=
，
∵
=
，
∴OC=
=
=
．
∴cos∠ACO=
=
=
．…（12分）
∴C1C⊥平面ABC，
又∵AD?平面ABC，∴C1C⊥AD，…（2分）
又点D是棱BC的中点，
且△ABC为正三角形，∴AD⊥BC，
∵BC∩C1C=C，∴AD⊥平面BCC1B1，…（4分）
又∵DC1?平面BCC1B1，∴AD⊥C1D．…（6分）
（2）过点C作CO⊥C1D，交C1D于点O．连结AO，
∵AD⊥平面BCC1B1，CO?平面BCC1B1，
∴CO⊥平面ADC1，…（8分）
∴∠ACO是直线AC与平面ADC1所成角，…（9分）
又∵∠COD=∠DCC1=90°，
∠ODC=∠ODC，
∴△ODC∽△DCC1．…（10分）
∵底面ABC是边长为2的正三角形，侧棱长为2，
且侧棱AA1⊥底面ABC，点D是BC的中点
∴DC=1，CC1=2，DC1=
| 1+4 |
| 5 |
∵
| OC |
| CC1 |
| DC |
| DC1 |
∴OC=
| DC•CC1 |
| DC1 |
| 1×2 | ||
|
2
| ||
| 5 |
∴cos∠ACO=
| OC |
| AC |
| ||||
| 2 |
| ||
| 5 |
点评：本题考查直线与直线垂直，直线与平面平行，考查空间想象能力，计算能力．
练习册系列答案
孟建平名校考卷系列答案
相关题目
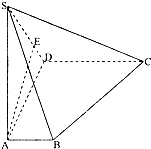如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AD垂直于AB和DC，侧棱SA⊥底面ABCD，且SA=2，AD=DC=1．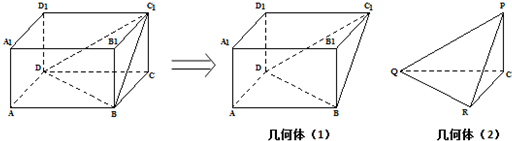
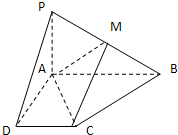已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=
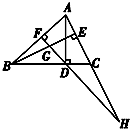如图，AD、BE是△ABC的高，DF⊥AB于F，DF交BE于G，FD的延长线交AC的延长线于H，求证：DF2=FG•FH．
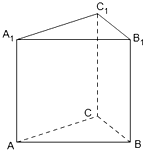如图，已知A，B，C为不在同一直线上的三点，且AA1∥BB1∥CC1，AA1=BB1=CC1．