题目内容
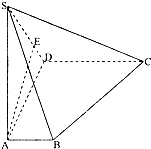 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1.(1)若点E在SD上,且AE⊥SD,证明:AE⊥平面SDC;
(2)若三棱锥S-ABC的体积VS-ABC=
| 1 |
| 6 |
考点:用空间向量求平面间的夹角,直线与平面垂直的判定,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明AE⊥平面SDC,只需证明AE⊥CD,利用证明CD⊥侧面SAD可得;
(2)连结AC,利用三棱锥S-ABC的体积VS-ABC=
,求出AB,再建立坐标系,求出平面SAD的一个法向量、平面SBC的一个法向量,利用向量的夹角公式,即可求面SAD与面SBC所成二面角的正弦值大小.
(2)连结AC,利用三棱锥S-ABC的体积VS-ABC=
| 1 |
| 6 |
解答:
 (1)证明:∵侧棱SA⊥底面ABCD,CD?底面ABCD,
(1)证明:∵侧棱SA⊥底面ABCD,CD?底面ABCD,
∴SA⊥CD.….(1分)
∵底面ABCD直角梯形,AD垂直于AB和DC,
∴AD⊥CD,
又AD∩SA=A,
∴CD⊥侧面SAD,….(3分)
∵AE?侧面SAD
∴AE⊥CD,
∵AE⊥SD,CD∩SD=D,
∴AE⊥平面SDC;….(5分)
(2)解:连结AC,
∵底面ABCD直角梯形,AD垂直于AB和DC,SA=2,AD=DC=1
∴AC=
,∠ACB=
,
设AB=t,则S△ABC=
AC•t=
,
∵三棱锥V=
=
•
,
∴t=AB=
.….(7分)
如图建系,则A(0,0,0),S(0,0,2),D(0,1,0),B(0.5,0,0),C(1,1,0),
由题意平面SAD的一个法向量为
=(1,0,0),
不妨设平面SBC的一个法向量为
=(x,y,z),则
∵
=(0.5,0,-2),
=(1,1,-2),
∴
,
不妨令z=1,则
=((4,-2,1)….(10分)
∴cos<
,
>=
=
,….(11分)
设面SAD与面SBC所成二面角为θ,则sinθ=
….(12分)
 (1)证明:∵侧棱SA⊥底面ABCD,CD?底面ABCD,
(1)证明:∵侧棱SA⊥底面ABCD,CD?底面ABCD,∴SA⊥CD.….(1分)
∵底面ABCD直角梯形,AD垂直于AB和DC,
∴AD⊥CD,
又AD∩SA=A,
∴CD⊥侧面SAD,….(3分)
∵AE?侧面SAD
∴AE⊥CD,
∵AE⊥SD,CD∩SD=D,
∴AE⊥平面SDC;….(5分)
(2)解:连结AC,
∵底面ABCD直角梯形,AD垂直于AB和DC,SA=2,AD=DC=1
∴AC=
| 2 |
| π |
| 4 |
设AB=t,则S△ABC=
| ||
| 4 |
| t |
| 2 |
∵三棱锥V=
| 1 |
| 6 |
| 2 |
| 3 |
| t |
| 2 |
∴t=AB=
| 1 |
| 2 |
如图建系,则A(0,0,0),S(0,0,2),D(0,1,0),B(0.5,0,0),C(1,1,0),
由题意平面SAD的一个法向量为
| m |
不妨设平面SBC的一个法向量为
| n |
∵
| SB |
| SC |
∴
|
不妨令z=1,则
| n |
∴cos<
| m |
| n |
| ||||
|
|
| 4 | ||
|
设面SAD与面SBC所成二面角为θ,则sinθ=
| ||
| 21 |
点评:本题考查线面垂直的判断与性质,考查面面角,考查三棱锥体积的计算,考查向量法的运用,正确求出平面的法向量是关键.

练习册系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1中,E是AB的中点
如图,正方体ABCD-A1B1C1D1中,E是AB的中点 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2 如图:三棱柱A1B1C1-ABC,A1A⊥AC,A1A⊥AB,AB=AC=1,A1B=2,E是A1B的中点.
如图:三棱柱A1B1C1-ABC,A1A⊥AC,A1A⊥AB,AB=AC=1,A1B=2,E是A1B的中点. 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为2,且侧棱AA1⊥底面ABC,点D是BC的中点
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为2,且侧棱AA1⊥底面ABC,点D是BC的中点 如图,点C为半圆的直径AB延长线上一点,AB=BC=2,过动点P作半圆的切线PQ,若
如图,点C为半圆的直径AB延长线上一点,AB=BC=2,过动点P作半圆的切线PQ,若