题目内容
以直角坐标系的原点为极点O,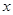 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为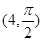 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为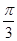 ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
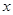 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为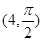 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为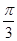 ,圆C的半径为4.
,圆C的半径为4.(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
(1) ,
, ;(2)直线
;(2)直线 与圆
与圆 相离.
相离.
 ,
, ;(2)直线
;(2)直线 与圆
与圆 相离.
相离.试题分析:本题主要考查直线的参数方程、极坐标方程、点到直线的距离公式、直线与圆的位置关系等基础知识,意在考查考生的运算求解能力、推理论证能力以及转化思想的应用.第一问,利用已知条件列出直线的参数方程,利用极坐标与直角坐标的转化公式,得到点C的直角坐标,从而得到圆C的标准方程,再利用极坐标与直角坐标的转化公式得到圆C的极坐标方程;第二问,将直线
 的参数方程先转化成普通方程,利用点到直线的距离公式求出距离,与半径比较大小,来判断直线与圆的位置关系.
的参数方程先转化成普通方程,利用点到直线的距离公式求出距离,与半径比较大小,来判断直线与圆的位置关系.试题解析:(1)直线
 的参数方程
的参数方程 ,即
,即 (
( 为参数)
为参数)由题知
 点的直角坐标为
点的直角坐标为 ,圆
,圆 半径为
半径为 ,
,∴圆
 方程为
方程为 将
将 代入
代入得圆
 极坐标方程
极坐标方程 5分
5分(2)由题意得,直线
 的普通方程为
的普通方程为 ,
,圆心
 到
到 的距离为
的距离为 ,
,∴直线
 与圆
与圆 相离. 10分
相离. 10分
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
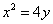 是否相切?说明理由.
是否相切?说明理由. :
:
 ,过定点
,过定点 作斜率为1的直线交圆
作斜率为1的直线交圆 、
、 两点,
两点, 为线段
为线段 的中点.
的中点. 的值;
的值; 为圆
为圆 面积的最大值;
面积的最大值; 向圆
向圆 ,且有
,且有 , 求
, 求 的最小值,并求
的最小值,并求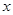 +4
+4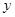 +8=0上的动点,PA、PB是圆
+8=0上的动点,PA、PB是圆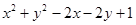 =0的两切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 .
=0的两切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值为 .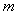 ,直线
,直线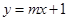 与圆
与圆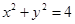 的位置关系一定是( )
的位置关系一定是( ) ,若
,若 ,则AB= .
,则AB= .
 是半圆
是半圆 :
: (
( )上一点,直线
)上一点,直线 的倾斜角为45°,过点
的倾斜角为45°,过点 轴的垂线,垂足为
轴的垂线,垂足为 ,过
,过 ,则直线
,则直线 的方程是 .
的方程是 . 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )


 上的点到直线
上的点到直线 的距离的最小值称为曲线
的距离的最小值称为曲线 到直线
到直线 的距离等于曲线
的距离等于曲线 到直线
到直线 _______.
_______.