题目内容
已知命题p:“∀x∈[1,2]都有x2≥a”.命题q:“∃x0∈R,使得x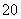 +2ax0+2-a=0成立”,若命题“p∧q”是真命题,则实数a的取值范围为( )
+2ax0+2-a=0成立”,若命题“p∧q”是真命题,则实数a的取值范围为( )
A.(-∞,-2] B.(-2,1)
C.(-∞,-2]∪{1} D.[1,+∞)
C 若p是真命题,即a≤(x2)min,x∈[1,2],所以a≤1;若q是真命题,即x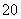 +2ax0+2-a=0有解,则Δ=4a2-4(2-a)≥0,即a≥1或a≤-2.命题“p∧q”是真命题,则p是真命题,q也是真命题,故有a≤-2或a=1.
+2ax0+2-a=0有解,则Δ=4a2-4(2-a)≥0,即a≥1或a≤-2.命题“p∧q”是真命题,则p是真命题,q也是真命题,故有a≤-2或a=1.

练习册系列答案
相关题目
 sin2x的最小正周期T为________.
sin2x的最小正周期T为________.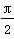 ,试判断p∨q,p∧q,綈p的真假性.
,试判断p∨q,p∧q,綈p的真假性. log2x,则f(2)=________.
log2x,则f(2)=________.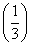 <f(2)<f
<f(2)<f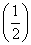
 的图像大致是( )
的图像大致是( )