题目内容
17.设$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$是两个不共线的向量,$\overrightarrow{AB}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$,$\overrightarrow{CB}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{CD}$=3$\overrightarrow{{e}_{1}}$-2k$\overrightarrow{{e}_{2}}$,若A,B,D共线,则k的值为( )| A. | -$\frac{9}{4}$ | B. | -$\frac{4}{9}$ | C. | -$\frac{3}{8}$ | D. | 不存在 |
分析 根据平面向量的线性运算法则,利用共线定理和向量相等列出方程组,即可求出k的值不存在.
解答 解:$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$是两个不共线的向量,且$\overrightarrow{AB}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$,$\overrightarrow{CB}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{CD}$=3$\overrightarrow{{e}_{1}}$-2k$\overrightarrow{{e}_{2}}$,
∴$\overrightarrow{BD}$=$\overrightarrow{CD}$-$\overrightarrow{CB}$=(3-k)$\overrightarrow{{e}_{1}}$-(2k+1)$\overrightarrow{{e}_{2}}$,
若A,B,D共线,
则$\overrightarrow{BD}$=λ$\overrightarrow{AB}$,
即(3-k)$\overrightarrow{{e}_{1}}$-(2k+1)$\overrightarrow{{e}_{2}}$=λ$\overrightarrow{{e}_{1}}$+2λ$\overrightarrow{{e}_{2}}$,
∴$\left\{\begin{array}{l}{3-k=λ}\\{-(2k+1)=2λ}\end{array}\right.$,
解得k的值不存在.
故选:D.
点评 本题考查了平面向量的线性运算与共线定理和向量相等的应用问题,是基础题目.

 阅读快车系列答案
阅读快车系列答案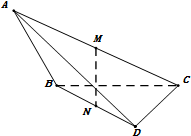 如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.
如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.