题目内容
x2-2x-5≥2x的解集是（ ）
| A、{x|x≥5或x≤-1} |
| B、{x|x＜-1或x＞5} |
| C、{x|-1≤x≤5} |
| D、{x|-1＜x＜5} |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：把原不等式化为一元二次不等式的一般形式再求解集．
解答：
解：原不等式可化为x2-4x-5≥0，
即（x+1）（x-5）≥0；
解得x≤-1或x≥5，
∴不等式的解集为{x|x≤-1或x≥5}．
故选：A．
即（x+1）（x-5）≥0；
解得x≤-1或x≥5，
∴不等式的解集为{x|x≤-1或x≥5}．
故选：A．
点评：本题考查了一元二次不等式的解法与应用问题，解题时应按照解一元二次不等式的基本步骤进行解答，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
sin13°cos47°+cos13°sin47°=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某学校有教师150人，其中高级教师15人，中级教师45人，初级教师90人．现按职称分层抽样选出30名教师参加教工代表大会，则选出的高、中、初级教师的人数分别为（ ）
| A、3，9，18 |
| B、5，10，15 |
| C、3，10，17 |
| D、5，9，16 |
命题“如果数列{an}的前n项和Sn=2n2-3n，那么数列{an}一定是等差数列”是否成立（ ）
| A、不成立 | B、成立 |
| C、不能断定 | D、能断定 |
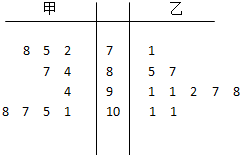两名射击运动员甲、乙在某次比赛中的成绩（单位：环）用茎叶图表示如图，甲、乙两人射击成绩的中位数分别用n甲、n乙表示，则（ ）| A、n甲＞n乙 |
| B、n甲＜n乙 |
| C、n甲=n乙 |
| D、n甲、n乙的大小关系不确定 |
已知z=1+i，
=1-i，则实数a，b的大小关系为（ ）
| z2az+b |
| z2-z+1 |
| A、a＞b | B、a＜b |
| C、a=b | D、大小关系无法确定 |
否定：“自然数a，b，c中恰有一个偶数”时正确的反设为（ ）
| A、a，b，c都是偶数 |
| B、a，b，c都是奇数 |
| C、a，b，c中至少有两个偶数 |
| D、a，b，c中都是奇数或至少有两个偶数 |