题目内容
6. 正方体ABCD-A1B1C1D1中,点E在棱CC1上,CE=2EC1,AB=6,M,N分别为棱AB和AD的中点.
正方体ABCD-A1B1C1D1中,点E在棱CC1上,CE=2EC1,AB=6,M,N分别为棱AB和AD的中点.(1)求三棱锥M-BDE的体积;
(2)求证:平面C1MN∥平面BDE.
分析 (I)VM-BDE=VE-BDM=$\frac{1}{3}$S△BDM•CE.
(II)连接AC与MN和BD分别交于F,G两点,连接C1F和EG,由中位线定理得MN∥BD,由$\frac{CG}{CF}=\frac{CE}{CC′}=2$得EG∥C1F,故平面C1MN∥平面BDE.
解答 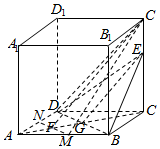 解:(Ⅰ)∵正方体ABCD-A1B1C1D1中,AB=6,CE=2EC1,
解:(Ⅰ)∵正方体ABCD-A1B1C1D1中,AB=6,CE=2EC1,
∴CE=4.
∵CE⊥平面BDM,
∴VM-BDE=VE-BDM=$\frac{1}{3}$S△BDM•CE=$\frac{1}{3}×\frac{1}{2}×3×6×4$=12.
(Ⅱ)连接AC与MN和BD分别交于F,G两点,连接C1F和EG.
∵M,N分别是AB和AD的中点,
∴MN∥BD,又∵MN?平面BDE,BD?平面BDE,
∴MN∥平面BDE.
∵$\frac{CE}{EC1}$=$\frac{CG}{GF}$=2,∴EG∥C1F,
又∵C1F?平面BDE,EG?平面BDE,
∴C1F∥平面BDE.
∵C1F?平面C1MN,MN?平面C1MN,C1F∩MN=F,
∴平面C1MN∥平面BDE.
点评 本题考查了面面平行的判定,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
 如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.
如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.