题目内容

20．若复数z满足z（2+i）=$\frac{10}{1+i}$，则z的共轭复数$\overline z$=（　　）
A．1+3iB．1-3iC．3+iD．3-i

分析 利用复数的运算法则、共轭复数的定义即可得出．

解答 解：复数z满足z（2+i）=$\frac{10}{1+i}$，∴z=$\frac{10（2-i）（1-i）}{（2+i）（2-i）（1+i）（1-i）}$=$\frac{10（1-3i）}{10}$=1-3i，
则z的共轭复数$\overline z$=1+3i．
故选：A．

点评 本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
20．求证：顺次连接A（2，-3），B（5，-$\frac{7}{2}$），C（2，3），D（-4，4）四点所得的四边形是梯形．
11．已知函数f（x）=x2-（-1）k2alnx（k∈N，a∈R且a＞0）．
（1）求f（x）的极值；
（2）若k=2016，关于x的方程f（x）=2ax有唯一解，求a的值．
8．分别求满足下列条件的直线l的方程：
（1）过点A（0，2），且直线l的倾斜角的正弦值是0.5；
（2）过点A（2，1），且直线l的倾斜角是直线l1：3x+4y+5=0的倾斜角的一半．
15．已知a＞b＞0，试指出$\frac{a+b}{2}$-$\sqrt{ab}$，$\frac{（a-b）^{2}}{8a}$，$\frac{（a-b）^{2}}{8b}$的大小关系，并给出证明．
5．直线l：x-2y+2=0过椭圆$\frac{x^2}{5}+\frac{y^2}{b^2}=1$$（0＜b＜\sqrt{5}）$的一个顶点．则该椭圆的离心率为（　　）
A．$\frac{1}{5}$B．$\frac{2}{5}$C．$\frac{{\sqrt{5}}}{5}$D．$\frac{{2\sqrt{5}}}{5}$
12．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点F与抛物线y2=4x的焦点重合，且椭圆的离心率为$\frac{\sqrt{3}}{3}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）椭圆C上是否存在关于直线l：x+y=$\frac{1}{5}$对称的两点A、B，若存在，求出直线AB的方程；若不存在，请说明理由．
9．已知定义在R上的函数f（x）的图象连续不断，若存在常数t（t∈R），使得f（x+t）+tf（x）=0对任意的实数x成立，则称f（x）是回旋函数．给出下列四个命题：
①常值函数f（x）=a（a≠0）为回旋函数的充要条件是t=-1；
②若f（x）=ax（0＜a＜1）为回旋函数，则t＞1；
③函数f（x）=x2不是回旋函数；
④若f（x）是t=2的回旋函数，则f（x）在[0，4032]上至少有2016个零点．
其中为真命题的是①③④．（写出所有真命题的序号）．
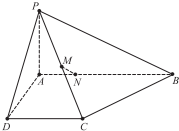10．如图，在四棱锥P-ABCD中，已知AB⊥AD，AD⊥DC．PA⊥底面ABCD，且AB=2，PA=AD=DC=1，M为PC的中点，N在AB上，且BN=3AN．
（1）求证：平面PAD⊥平面PDC；
（2）求证：MN∥平面PAD；
（3）求三棱锥C-PBD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网