题目内容
函数f(x)的定义域[-4,4],图象如图,则不等式
<0的解集为 .
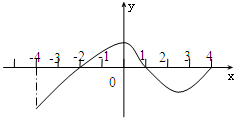
| f(x) |
| cos2x |

考点:其他不等式的解法
专题:计算题,函数的性质及应用,三角函数的图像与性质,不等式的解法及应用
分析:不等式
<0即为
或
,再由f(x)的图象和余弦函数的图象和性质,得到不等式组,对k取值,即可得到所求解集.
| f(x) |
| cos2x |
|
|
解答:
解:不等式
<0即为
或
,
即有
或
,(k∈Z),
即有
或
则
或
或
或
,
解得,
<x<1或-2<x<-
或
<x<
或-
<x<-
.
则解集为:(-
,-
)∪(-2,-
)∪(
,1)∪(
,
).
故答案为:(-
,-
)∪(-2,-
)∪(
,1)∪(
,
).
| f(x) |
| cos2x |
|
|
即有
|
|
即有
|
|
则
|
|
|
|
解得,
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
| 5π |
| 4 |
| 3π |
| 4 |
则解集为:(-
| 5π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
故答案为:(-
| 5π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
点评:本题考查不等式的解法,考查余弦函数的图象和性质,考查运算能力,属于中档题和易错题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
在等比数列{an}中,已知a1=2,a3•a5=16,则a7=( )
| A、16 | B、-8 | C、8 | D、-4 |
tan
=( )
| 5π |
| 6 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
设实数x,y满足不等式组
,则
的取值范围是( )
|
| y |
| x+3 |
A、[0,
| ||||
B、[
| ||||
C、[0,
| ||||
D、[
|
 如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.