题目内容
11.(Ⅰ)从{-3,-2,-1,0,1,2,3,4}中任选三个不同元素作为二次函数y=ax2+bx+c的系数,问能组成多少条经过原点且顶点在第一象限或第三象限的抛物线?(Ⅱ)已知($\frac{1}{2}$+2x)n,若展开式中第5项、第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项的系数.
分析 (Ⅰ)根据顶点在第一象限和顶点在第三象限两种情况分类讨论,求出结果.
(Ⅱ)第k+1项的二项式系数为Cnk,由题意可得关于n的方程,求出n.而二项式系数最大的项为中间项,n为奇数时,中间两项二项式系数相等;n为偶数时,中间只有一项.
解答 解:(Ⅰ)抛物线经过原点,得c=0,
当顶点在第一象限时,a<0,-$\frac{b}{2a}$>0,
即$\left\{\begin{array}{l}{a<0}\\{b>0}\end{array}\right.$,则有3×4=12(种);
当顶点在第三象限时,a>0,-$\frac{b}{2a}$<0,
即a>0,b>0,则有4×3=12(种);
共计有12+12=24(种).
(Ⅱ)∵Cn4+Cn6=2Cn5,
∴n2-21n+98=0,
∴n=7或n=14.
当n=7时,展开式中二项式系数最大的项是T4和T5,
∴T4的系数=C73($\frac{1}{2}$)423=$\frac{35}{2}$,
T5的系数=C74($\frac{1}{2}$)324=70.
当n=14时,展开式中二项式系数最大的项是T8.
∴T8的系数=C147($\frac{1}{2}$)727=3432.
点评 本题考查满足条件的抛2的条数的求法,考查二项展开式中二项式系数和与系数和问题,难度较大,易出错.要正确区分这两个概念.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
1.当x=$\frac{π}{4}$时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数y=f($\frac{3π}{4}$-x)是( )
| A. | 奇函数且图象关于直线x=$\frac{π}{2}$对称 | B. | 偶函数且图象关于点(π,0)对称 | ||
| C. | 奇函数且图象关于($\frac{π}{2}$,0)对称 | D. | 偶函数且图象关于点($\frac{π}{2}$,0)对称 |
2.设a>0,b>0,则“x>a且y>b”是“x+y>a+b,且xy>ab”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.已知向量$\overline{a}$=(1,-$\sqrt{3}$),$\overline{b}$=(-2,0),则$\overline{a}$与$\overline{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
3.已知△ABC的外接圆的圆心为O,半径为1,2$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{0}$,且|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|,则向量$\overrightarrow{AC}$在向量$\overrightarrow{BC}$方向上的投影为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
1.若y=f(x2),则y′等于( )
| A. | 2xf′(x2) | B. | 2xf′(x) | C. | 4x2f(x) | D. | f′(x2) |
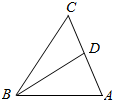 如图,在△ABC中,已知AB=3,BC=4,∠ABC=60°,BD为AC边上的中线.
如图,在△ABC中,已知AB=3,BC=4,∠ABC=60°,BD为AC边上的中线.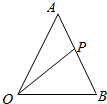 如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.
如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.