题目内容
10.下面给出的四个命题中:①以抛物线y2=4x的焦点为圆心,且过坐标原点的圆的方程为(x-2)2+y2=4;
②若m=-2,则直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直;
③命题“?x∈R,使得x2+3x+4=0”的否定是“?x∈R,都有x2+3x+4≠0”;
④将函数y=sin2x的图象向右平移$\frac{π}{3}$个单位,得到函数y=sin(2x-$\frac{π}{3}$)的图象.
其中是真命题的有②③(将你认为正确命题的序号都填上).
分析 ①求出抛物线的焦点,结合圆的方程进行求解.
②根据直线垂直的关系进行判断.
③根据含有量词的命题的否定进行判断.
④根据三角函数的图象关系进行判断.
解答 解:①∵抛物线y2=4x的焦点(1,0)
∴所求圆的圆心为(1,0)
又∵所求圆过坐标原点,∴所求圆的半径R=1
∴所求圆的方程为(x-1)2+y2=1,故①错误,
②若m=-2,则两条直线方程为-2y+1=0与-4x-3=0,满足相互垂直;故②正确,
③命题“?x∈R,使得x2+3x+4=0”的否定是“?x∈R,都有x2+3x+4≠0”;正确,故③正确,
④将函数y=sin2x的图象向右平移$\frac{π}{3}$个单位,得到函数y=sin2(x-$\frac{π}{3}$)的图象.故④错误,
故答案为:②③
点评 本题主要考查命题的真假判断,涉及知识点较多,综合性较强,但难度不大.

练习册系列答案
相关题目
18.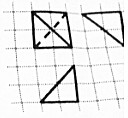 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是一个四面体的三视图,则该四面体外接球的体积与四面体的体积的比值为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是一个四面体的三视图,则该四面体外接球的体积与四面体的体积的比值为( )
 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是一个四面体的三视图,则该四面体外接球的体积与四面体的体积的比值为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是一个四面体的三视图,则该四面体外接球的体积与四面体的体积的比值为( )| A. | 2$\sqrt{2}$π | B. | 3$\sqrt{3}$π | C. | 4π | D. | 2$\sqrt{5}$π |
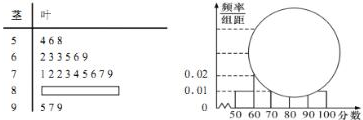 某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;
某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;
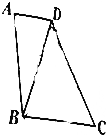 在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.
在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.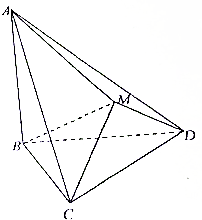 如图,△BCD与△MCD都是正三角形,平面MCD⊥平面BCD,AB⊥平面BCD.
如图,△BCD与△MCD都是正三角形,平面MCD⊥平面BCD,AB⊥平面BCD.