题目内容
19.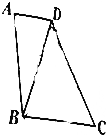 在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.
在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.
分析 过D作DE⊥BC于E,连结A′E,过A′作A′O⊥DE,连结A′O.则可证明A′O⊥平面BCD,于是∠A′BO为直线A′B与平面BCD所成的角.设AD=1,在直角梯形中根据平面几何知识解出DO,从而得出A′O,得出线面角的正弦值.
解答 解:过D作DE⊥BC于E,连结A′E,过A′作A′O⊥DE,连结A′O.
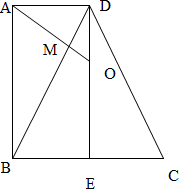 ∵BC⊥A′D,BC⊥DE,A′D∩A′O=A′,
∵BC⊥A′D,BC⊥DE,A′D∩A′O=A′,
∴BC⊥平面A′DE,∵A′O?平面A′DE,
∴BC⊥A′O,又A′O⊥DE,BC∩DE=E,
∴A′O⊥平面BCD.
∴∠A′BO为直线A′B与平面BCD所成的角.
在直角梯形ABCD中,过A作AO⊥BD,交BD于M,交DE于O,
设AD=1,则AB=2,∴BD=$\sqrt{5}$,
∴AM=$\frac{AB•AD}{BD}$=$\frac{2}{\sqrt{5}}$,∴DM=$\sqrt{A{D}^{2}-A{M}^{2}}$=$\frac{1}{\sqrt{5}}$.
由△AMD∽△DMO得$\frac{DM}{AM}=\frac{OD}{AD}$,即$\frac{\frac{1}{\sqrt{5}}}{\frac{2}{\sqrt{5}}}=\frac{DO}{1}$,∴DO=$\frac{1}{2}$.
∴A′O=$\sqrt{A′{D}^{2}-D{O}^{2}}$=$\frac{\sqrt{3}}{2}$.
∴sin∠A′BO=$\frac{A′O}{A′B}$=$\frac{\frac{\sqrt{3}}{2}}{2}=\frac{\sqrt{3}}{4}$.
故答案为$\frac{\sqrt{3}}{4}$.
点评 本题考查了线面角的作法与计算,根据条件构造线面垂直得出线面角是解题关键.

练习册系列答案
相关题目
4.已知函数f(x)的定义域为R,且f′(x)+f(x)=2xe-x,若f(0)=1,则函数$\frac{f′(x)}{f(x)}$的取值范围为( )
| A. | [-2,0] | B. | [-1,0] | C. | [0,1] | D. | [0,2] |
8.等差数列{an}中,若a5=7,则( )
| A. | S9=63 | B. | S11=63 | C. | S9=35 | D. | S11=77 |