题目内容
若等腰直角三角形的直角边长为2,则以斜边所在的直线为轴旋转一周所成的几何体体积是 .
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:画出图形,根据圆锥的体积公式直接计算即可.
解答:
解:如图为等腰直角三角形旋转而成的旋转体.
V=2×
S•h=
πR2•h
=2×
π×(
)2×
=
.
故答案为:
.

V=2×
| 1 |
| 3 |
| 1 |
| 3 |
=2×
| 1 |
| 3 |
| 2 |
| 2 |
4
| ||
| 3 |
故答案为:
4
| ||
| 3 |
点评:本题考查圆锥的体积公式,是基础题.

练习册系列答案
相关题目
已知△ABC的顶点A(0,0),B(4,0),且AC边上的中线BD的长为3,则顶点C的轨迹方程是( )
| A、(x-8)2+y2=36(y≠0) |
| B、(x-4)2+y2=9(y≠0) |
| C、x2+y2=9(y≠0) |
| D、3x+4y-12=0(y≠0) |
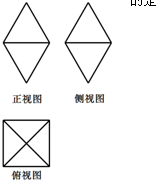 如图是某宝石饰物的三视图,已知该饰物的正视图、侧视图都是面积为
如图是某宝石饰物的三视图,已知该饰物的正视图、侧视图都是面积为