题目内容
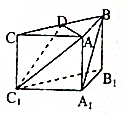 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=AA1,D为BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=AA1,D为BC的中点.(1)证明:A1B∥平面ADC1;
(2)证明:平面ADC1⊥平面BB1C1C.
考点:向量语言表述面面的垂直、平行关系,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)以A1为原点,A1C1为x轴,A1B1为y轴,A1A为z轴,建立空间直角坐标系,求出向量
=(0,2,2)和平面ADC1的法向量,由
•
=0,且A1B?平面ADC1,能证明A1B∥平面ADC1.
(2)分别求出平面BB1C1C的法向量和平面ADC1的法向量,由两个平面的法向量的数量积为0,能证明平面ADC1⊥平面BB1C1C.
| A1B |
| n |
| A1B |
(2)分别求出平面BB1C1C的法向量和平面ADC1的法向量,由两个平面的法向量的数量积为0,能证明平面ADC1⊥平面BB1C1C.
解答:
(1)证明:∵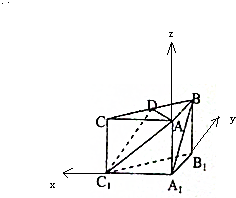 在直三棱柱ABC-A1B1C1中,AB⊥AC,
在直三棱柱ABC-A1B1C1中,AB⊥AC,
∴以A1为原点,A1C1为x轴,A1B1为y轴,A1A为z轴,
建立空间直角坐标系,设AB=AC=AA1=2,
A1(0,0,0),B(0,2,2),A(0,0,2),
C(2,0,2),D(1,1,2),C1(2,0,0),
=(0,2,2),
=(1,1,0),
=(2,0,-2),
设平面ADC1的法向量
=(x,y,z),
则
,取x=1,得
=(1,-1,1),
∵
•
=0-2+2=0,且A1B?平面ADC1,
∴A1B∥平面ADC1.
(2)证明:∵
=(1,-1,0),
=(1,-1,-2),
设平面BB1C1C的法向量
=(a,b,c),
则
,取a=1,得
=(1,1,0),
又平面ADC1的法向量
=(1,-1,1),
•
=1-1+0=0,
∴平面ADC1⊥平面BB1C1C.
 在直三棱柱ABC-A1B1C1中,AB⊥AC,
在直三棱柱ABC-A1B1C1中,AB⊥AC,∴以A1为原点,A1C1为x轴,A1B1为y轴,A1A为z轴,
建立空间直角坐标系,设AB=AC=AA1=2,
A1(0,0,0),B(0,2,2),A(0,0,2),
C(2,0,2),D(1,1,2),C1(2,0,0),
| A1B |
| AD |
| AC1 |
设平面ADC1的法向量
| n |
则
|
| n |
∵
| n |
| A1B |
∴A1B∥平面ADC1.
(2)证明:∵
| DC |
| DC1 |
设平面BB1C1C的法向量
| m |
则
|
| m |
又平面ADC1的法向量
| n |
| n |
| m |
∴平面ADC1⊥平面BB1C1C.
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
一批热水器共有98台,其中甲厂生产的有56台,乙厂生产的有42台,用分层抽样从中抽取一个容量为14的样本,那么甲、乙两厂各抽取的热水器的台数是( )
| A、9,5 | B、8,6 |
| C、10,4 | D、7,7 |
已知点P是双曲线
-y2=1上任意一点,过点P分别作双曲线的两条渐近线的垂线,垂足分别为A、B,则
•
=( )
| x2 |
| 4 |
| PA |
| PB |
A、-
| ||
B、
| ||
C、-
| ||
D、-
|
已知m,n为异面直线,m?平面α,n?平面β,α∩β=l,则直线l( )
| A、与m,n 都相交 |
| B、至多与m,n 中的一条相交 |
| C、与m,n 都不相交 |
| D、与m,n 至少一条相交 |
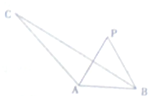 如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.
如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.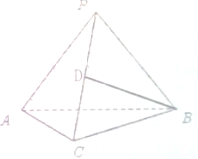 如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,且PA=PC=2.
如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,且PA=PC=2. 一个正方体挖去一个圆锥得到一个几何体,其正视图与俯视图如图所示,则该几何体的侧(左)视图是( )
一个正方体挖去一个圆锥得到一个几何体,其正视图与俯视图如图所示,则该几何体的侧(左)视图是( )


